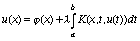 . (55)
. (55)
УДК 519.6
Рассмотрим нелинейное интегральное уравнение вида
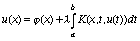 . (55)
. (55)
Пусть функция (x)C[a,b], а функция K(x,t,u) - непрерывная функция своих аргументов при x,t[a,b], - < u < . Кроме того, функция K(x,t,u) удовлетворяет условию Липшица по переменной u:
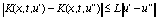 ,
,
где L = const, не зависящая
от выбора u', u". Как известно, (см., например [6])
при 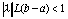 существует единственное решение
уравнения (55) и оно может быть найдено методом последовательных
приближений. Поскольку при реализации этого метода требуется вычислять
интегралы, что, как правило, нельзя сделать точно, то рассмотрим
алгоритм, который позволляет обходить эту трудность.
существует единственное решение
уравнения (55) и оно может быть найдено методом последовательных
приближений. Поскольку при реализации этого метода требуется вычислять
интегралы, что, как правило, нельзя сделать точно, то рассмотрим
алгоритм, который позволляет обходить эту трудность.
Приведем некоторые обозначения и факты,необходимые для дальнейшего. Пусть N 4 - целое положительное число, - разбиение отрезка [a,b] c шагом h, т. е.
 .
.
Пусть 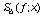 есть интерполяционный
кубический сплайн для функции f(x), построенный
по сетке c использованием концевых условий,
есть интерполяционный
кубический сплайн для функции f(x), построенный
по сетке c использованием концевых условий,
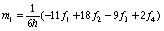 ,
,
 , fi = f(xi).
, fi = f(xi).
Эти формулы являются 4-точечными формулами приближенного дифференцирования (см., например [7]). Будем использовать такую формулу (см.[12] c.235)
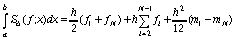 ,
,
где m1 и mN определены выше. Здесь предлагается следующий алгоритм нахождения приближенного решения уравнения (55)
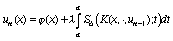 , (56)
, (56)
uo(x) = (x), n = 1,2,...,
где 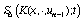 есть интерполяционный
кубический сплайн по переменной t, построенный для функции
K (x,t,un-1(t))
по сетке .
есть интерполяционный
кубический сплайн по переменной t, построенный для функции
K (x,t,un-1(t))
по сетке .
В пространстве C[a,b] достаточным условием сходимости алгоритма (56) является выполнение неравенства q < 1, где
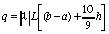 ,
,L - указанная выше константа Липшица.
Проводя рассуждения, подобные тем, что были проведены в [1] для линейного случая, получаем априорную оценку погрешности, возникающей после n итераций. Пусть u(x) - точное решение уравнения (55), а un(x) - приближенное решение, полученное алгоритмом (56) после n итераций, тогда
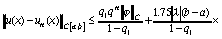
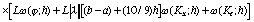 ,
,
где 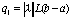 , (; h) -
модуль непрерывности функции (x), т.е.
, (; h) -
модуль непрерывности функции (x), т.е.
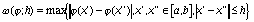 ,
,
(Kx;
h), и (Kt, h) - частные
модули непрерывности [8] функции K(x,t,u) соответственно
по переменным x и t. Отметим, что при h 0
имеем q q1, (, h) 0,
(Kx; h) 0,
(Kt; h) 0
и поэтому указанная выше оценка переходит в оценку, получаемую
при применении метода последовательных приближений. Алгоритм вида
(56) в двумерном случае построен и исследован как при использовании
двумерных интерполяционных бикубических сплайнов, так и, учитывая
соображения из [13], с использованием локальных двумерных сплайнов.
Эти алгоритмы реализованы на ПК и показали хорошую эффективность.
При использовании интерполяционных бикубических сплайнов в двумерном
линейном случае алгоритм вида (56) исследован в [1].
Рассмотрим систему нелинейных интегральных уравнений вида
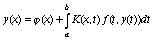 , (57)
, (57)
где
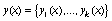 ,
, 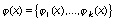 ,
,
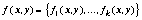
есть вектор-функции со значением в евклидовом пространстве
R k; 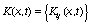 - квадратная
матрица размерности k k, причем
- квадратная
матрица размерности k k, причем
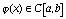 ,
, 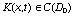 ,
,
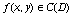 ,
,
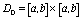 ,
, 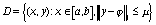 ,
,
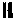 - норма вектора в пространстве
Rk. Оператор, определяемый правой частью уравнения
(57), действует в пространстве C[a,b] непрерывных
вектор-функций с нормой
- норма вектора в пространстве
Rk. Оператор, определяемый правой частью уравнения
(57), действует в пространстве C[a,b] непрерывных
вектор-функций с нормой
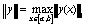 .
.
Для приближенного решения системы (57) используем алгоритм
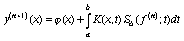 ,
, 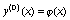 ,
(58)
,
(58)
где 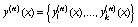 , f(n)(x) = f(x, y(n)(x)),
S(g,x) - кубический вектор-сплайн дефекта 1, интерполирующий
покоординатно вектор g(x) в узлах равномерной сетки
,
, f(n)(x) = f(x, y(n)(x)),
S(g,x) - кубический вектор-сплайн дефекта 1, интерполирующий
покоординатно вектор g(x) в узлах равномерной сетки
,
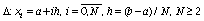 .
.
В (58) для сплайна S(g,x) используется
его представление через моменты 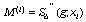 с краевыми
условиями
с краевыми
условиями
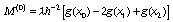 ,
,
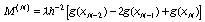 (59)
(59)
или через наклоны 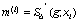 с краевыми
условиями
с краевыми
условиями
 ,
, 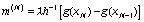 ,
(60)
,
(60)
где M(i) и (m(i) - k)-мерные
векторы, а параметр удовлетворяет условию  в соотношении (59) и = 1 в соотношениях (60).
в соотношении (59) и = 1 в соотношениях (60).
При обосновании алгоритма (58) используется следующее утверждение:
Если вектор-сплайн S(g,x) интерполирует вектор-функцию g(x) C[a,b] в узлах равномерной сетки и удовлетворяет краевому условию (59) или (60), то имеют место оценки
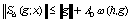 ,
, 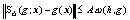 ,
(61)
,
(61)
где  , A = 1 + A0,
0 < (N) < 1, (h,g)
- модуль непрерывности вектор-функции g(x) на [a,b],
, A = 1 + A0,
0 < (N) < 1, (h,g)
- модуль непрерывности вектор-функции g(x) на [a,b],
 .
.
Для доказательства этого утверждения достаточно перенести на векторный случай методику работы [35] и использовать представление для S(g,x) через M(i) или через m(i) [4]. В одномерном случае соотношение (61) уточняет соответствующие результаты,содержащиеся в [14] и [9], и согласуется с результатами [12], а также [15],отнесенными к нулевым краевым условиям.
Обоснование алгоритма (58) проведено при следующих
дополнительных предположениях относительно заданных функций. Пусть
вектора  и
и  , а
также матрицы
, а
также матрицы 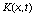 и
и 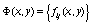 в соответствующих областях определения удоветворяют условиям:
в соответствующих областях определения удоветворяют условиям:
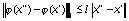 ,
, 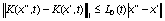 ,
,
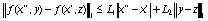 ,
,
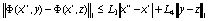 ,
,
где 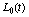 - интегрируемая на
- интегрируемая на 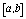 функция,
функция, 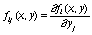 . Константы
. Константы 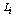 ,
,
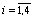 вообще-то зависят от . Вводя обозначения
вообще-то зависят от . Вводя обозначения
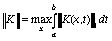 ,
, 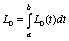 ,
,
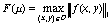 ,
, 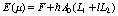
и подчиняя шаг сетки h условию 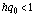 ,
,
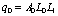 , определим как положительное
решение неравенства
, определим как положительное
решение неравенства
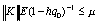 . (62)
. (62)
Тогда, как показано в [36], все последовательные
приближения 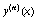 , определяемые соотношеием
(58), не выходят из области D, т.е.
, определяемые соотношеием
(58), не выходят из области D, т.е. 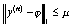 при
при 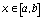 , n = 0,1,....
, n = 0,1,....
Показано, что алгоритм (58) сходится, если выполняется условие
 , (63)
, (63)
где 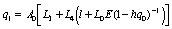 .
.
Установлено также, что оценка погрешности алгоритма (58) имеет вид
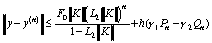 ,
, 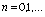 , (64)
, (64)
где
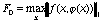 ,
,
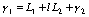 ,
, 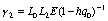 ,
,
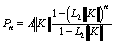 ,
, 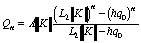 .
.
В (64) первое слагаемое характеризует оценку погрешности
обычного метода последовательных приближений, а второе - оценку
погрешности, обусловленную сплайн-аппроксимацией за n итераций,
причем  при
при 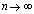 .
.
Из (64) можно заключить, что область сходимости алгоритма
(58) совпадает с областью сходимости метода простой итерации,
поскольку при выполнении условия 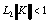 всегда
можно указать шаг сетки h, при котором будет выполняться
и условие (63).
всегда
можно указать шаг сетки h, при котором будет выполняться
и условие (63).
Алгоритм, изложенный выше, применим к решению систем нелинейных интегральных уравнений вида
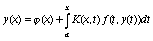 , (65)
, (65)
где заданные вектор-функции (x), f(x,y)
и матрица K(x,t) определены и непрерывны соответственно
в областях: [a,b], 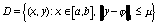 ,
, 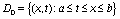 .
.
Алгоритм (58) применительно к системе (65) имеет вид
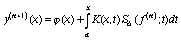 ,
, 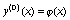 .
(66)
.
(66)
Предполагая, что вектор-функции (x), f(x,y)
и матрицы 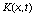 ,
, 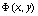 в
соответствующих областях определения удовлетворяют тем же условиям,
что и в предыдущем пункте, можно показать, что все последовательные
приближения (66) не выходят из области D, если определяется
неравенством (62). Заметим, что в этом случае константа Lo
подчинена неравенству
в
соответствующих областях определения удовлетворяют тем же условиям,
что и в предыдущем пункте, можно показать, что все последовательные
приближения (66) не выходят из области D, если определяется
неравенством (62). Заметим, что в этом случае константа Lo
подчинена неравенству
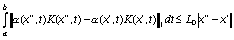 ,
,
где 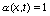 при
при 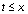 и
и 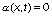 при
при  .
.
Можно показать, что если шаг сетки вектор-сплайна удовлетворяет условию
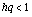 ,
, 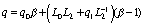 ,
(67)
,
(67)
то алгоритм (66) сходится равномерно по 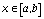 к некоторой непрерывной функции и имеет место оценка погрешности:
к некоторой непрерывной функции и имеет место оценка погрешности:
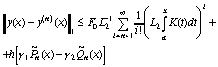 , (68)
, (68)
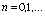 ,
,
где
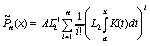 ,
,
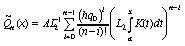 ,
,
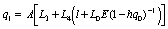 ,
, 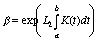 ,
,
причем 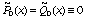 и
и  при
при 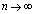 равномерно относительно
равномерно относительно 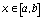 .
Остальные константы, входящие в оценку (68), определяются так
же, как в предыдущем пункте. В одномерном случае алгоритм (66)
рассмотрен и обоснован в работе [11].
.
Остальные константы, входящие в оценку (68), определяются так
же, как в предыдущем пункте. В одномерном случае алгоритм (66)
рассмотрен и обоснован в работе [11].
Как уже упоминалось выше, в формулах (9)-(11) необходимо
аппроксимировать функции двух переменных 1(x,y)
и 2(x,y). Применим для этого аппарат билинейных
сплайн-функций. Воспользуемся представлением этих функций через
сплайны первой степени двух переменных [12]. Тогда приближенные
значения 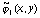 ,
, 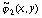 можно
записать в виде
можно
записать в виде
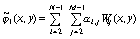 , (69)
, (69)
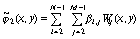 , (70)
, (70)
где введены следующие обозначения
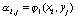 ,
, 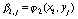 ,
,
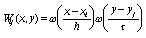 ,
,
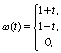
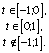
Учитывая, что
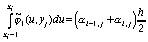 ,
,
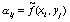 ,
,
из выражений (10), (11) получаем расчетные формулы вида
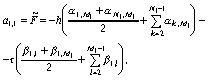 ,
,
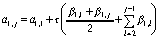 ,
, 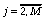 ,
,
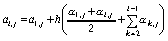 ,
,
 ,
, 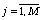 .
(84)
.
(84)
Полученные выражения (71) позволяют вычислять приближенные
значения 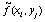 искомой функции
искомой функции 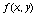 в узлах сетки . Погрешность вычисления функции
в узлах сетки . Погрешность вычисления функции 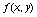 можно оценить следующим образом:
можно оценить следующим образом:
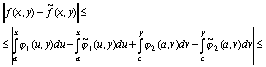
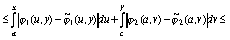
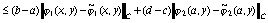
Таким образом, достаточно иметь оценку погрешности
приближения функций 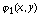 и
и 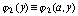 сплайнами
сплайнами 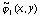 и
и 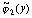 соответственно. Предыдущая цепочка неравенств получена в предположении,
что
соответственно. Предыдущая цепочка неравенств получена в предположении,
что 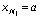 ,
, 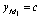 . Хорошо
известно [4], что если
. Хорошо
известно [4], что если 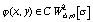 , то
, то
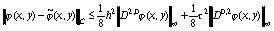
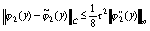 ,
,
где 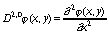 ,
, 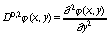 .
.
Следовательно, окончательно имеем
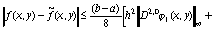
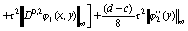 (72)
(72)
В ряде экспериментальных ситуаций, когда шаги 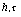 сетки фиксированы, погрешность вычисления функции
сетки фиксированы, погрешность вычисления функции 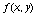 по формулам (71) порядка
по формулам (71) порядка 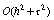 оказывается
неприемлемо высокой. Для получения расчетных формул с погрешностью
вычислений четвертого порядка относительно шагов сетки используем
интерполяционные кубические сплайны.
оказывается
неприемлемо высокой. Для получения расчетных формул с погрешностью
вычислений четвертого порядка относительно шагов сетки используем
интерполяционные кубические сплайны.
Исходя из того, что в формулах (10) фигурируют одномерные интегралы, введем в рассмотрение одномерные интерполяционные кубические сплайны следующим образом [4]:
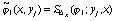 ,
, 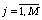
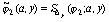 ,
,
т.е. для каждого фиксированного значения 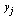 на сетке
на сетке 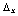 строится кубический сплайн
строится кубический сплайн 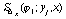 ,
а при
,
а при 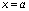 - сплайн
- сплайн 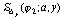 ,
удовлетворяющие условиям
,
удовлетворяющие условиям
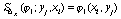 ,
, 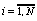 (73)
(73)
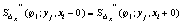 ,
,  (74)
(74)
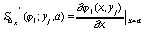 ,
,
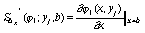 , (76)
, (76)
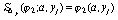 ,
,  ;
;
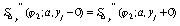 ,
, 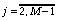 ,
(77)
,
(77)
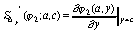 ,
,
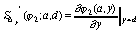 . (78)
. (78)
Для определения были использованы краевые условия (75),(78) типа I. Введем обозначения:
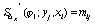 ,
, 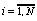 ,
,
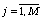 ,
,
 ;
; 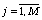 .
.
Раскрывая условия (73)-(78), получим M + 1 систему линейных уравнений с трехдиагональными матрицами:
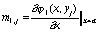 ,
, 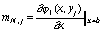 ,
,
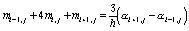 ,
, 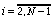 ;
(79)
;
(79)
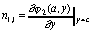 ,
, 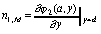 ,
,
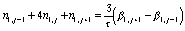 ,
, 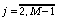 .
(80)
.
(80)
При этом учитывались конструкции
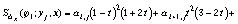
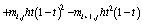 , (81)
, (81)
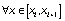 ,
, 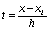 ,
,
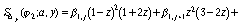
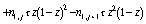 , (82)
, (82)
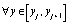 ,
, 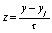 .
.
Решения систем (79), (80) относительно 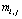 ,
,
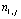 находятся методом прогонки. Учитывая,
что
находятся методом прогонки. Учитывая,
что
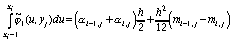 , (83)
, (83)
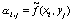 ,
,
получаем расчетные формулы вида:
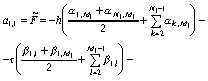
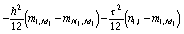 ,
,
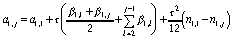 ,
, 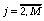 ,
,
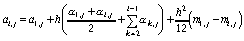 , (84)
, (84)
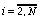 ;
;  .
Погрешность вычисления
.
Погрешность вычисления  оцениваем следующим
образом. Из [12] известно, что если
оцениваем следующим
образом. Из [12] известно, что если 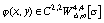 ,
то
,
то
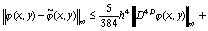
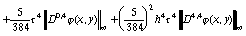
Отсюда следует, что
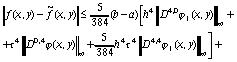
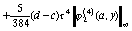 ,
, 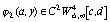 .
(85)
.
(85)
Применение интерполяционных кубических сплайнов позволяет
получить расчетные формулы с погрешностью 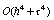 .
Однако повышение точностimgи вычислений при этом в сравнении с формулами
билинейной сплайн-интерполяции ведет к существенному увеличению
времени вычисления искомой функции в узлах сетки, поскольку возникает
необходимость решения
.
Однако повышение точностimgи вычислений при этом в сравнении с формулами
билинейной сплайн-интерполяции ведет к существенному увеличению
времени вычисления искомой функции в узлах сетки, поскольку возникает
необходимость решения 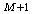 систем линейных
алгебраических уравнений (79),(80) относительно
систем линейных
алгебраических уравнений (79),(80) относительно 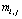 ,
,
 . Компромиссным вариантом между билинейной
сплайн-интерполяцией с погрешностью вычислений
. Компромиссным вариантом между билинейной
сплайн-интерполяцией с погрешностью вычислений 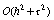 и малым временем вычислений и кубической сплайн-интерполяцией
с погрешностью порядка
и малым временем вычислений и кубической сплайн-интерполяцией
с погрешностью порядка 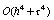 и большим временем
вычислений может служить способ, основанный на аппроксимации функций
локальными кубическими сплайнами минимального дефекта (см.[12,
13, 2, 3]). При таком подходе отпадает необходимость решения
систем линейных алгебраических уравнений и сохраняется четвертый
относительно h порядок погрешности вычислений, хотя константы,
определяющие величину погрешности,увеличиваются в 2-3 раза. Так,
например, если функция
и большим временем
вычислений может служить способ, основанный на аппроксимации функций
локальными кубическими сплайнами минимального дефекта (см.[12,
13, 2, 3]). При таком подходе отпадает необходимость решения
систем линейных алгебраических уравнений и сохраняется четвертый
относительно h порядок погрешности вычислений, хотя константы,
определяющие величину погрешности,увеличиваются в 2-3 раза. Так,
например, если функция 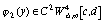 приближается кубическим
интерполяционным сплайном
приближается кубическим
интерполяционным сплайном 
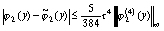 .
.
Погрешность приближения функции 
 ,
,
при условии, что 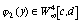 . Приступая
к получению расчетных формул, сделаем следующие предположения
относительно сетки
. Приступая
к получению расчетных формул, сделаем следующие предположения
относительно сетки 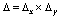 . Будем считать, что
сетка накрыта сеткой
. Будем считать, что
сетка накрыта сеткой  такой, что
такой, что 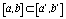 ,
,
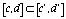 . При этом на каждом из отрезков
. При этом на каждом из отрезков 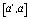 ,
,
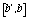 ,
, 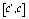 ,
, 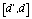 размещается по три узла сетки. В узлах сетки
размещается по три узла сетки. В узлах сетки  определены значения функций
определены значения функций 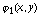 ,
, 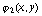 .
.
По аналогии с предыдущим пунктом введем в рассмотрение
одномерные локальные аппроксимационные кубические сплайны [12]:
при 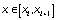
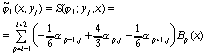 , (86)
, (86)
при 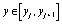
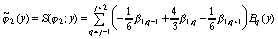 ,
,
где 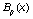 - кубические В-сплайны,
определяемые на отрезке
- кубические В-сплайны,
определяемые на отрезке 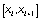 формулами
формулами
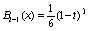 ,
,
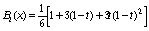 ,
,
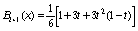 , (87)
, (87)
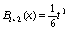 ,
, 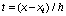 .
.
Формулы (86) являются точными на кубических многочленах.
Выражения для 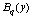 аналогичны формулам (87).
Поскольку
аналогичны формулам (87).
Поскольку
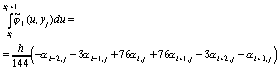 ,
,то расчетные формулы в соответствии с (10) имеют вид:

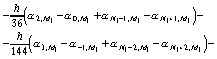
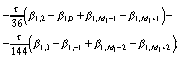
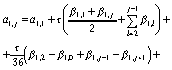
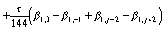 ;
; 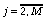 ;
;
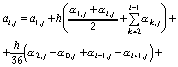
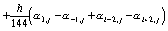 ;
;
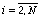 ;
; 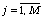 .
(88)
.
(88)
Сопоставляя формулы (71), (84) и (88), видим,что
выражения (84) и (88) являются уточненными по сравнению с (71).
Однако уточнение по (84) достигается за счет решения 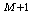 систем линейных алгебраических уравнений (79), (80) относительно
систем линейных алгебраических уравнений (79), (80) относительно
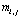 ,
, 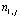 .
.
Для вычисления по формулам (88) требуется лишь знание
значений функций 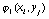 и
и 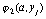 в узлах сетки
в узлах сетки 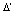 . Можно показать,что погрешность
вычисления
. Можно показать,что погрешность
вычисления 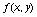 по формулам (88) имеет порядок
по формулам (88) имеет порядок
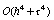 , если
, если 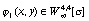 ,
, 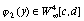 .
.
Разработанные алгоритмы моделирования с использованием
математического аппарата сплайн-функций вне всякого сомнения являются
мощным средством для решения широкого круга исследовательских
задач биологии, медицины и экологии.
Developed algorithms for a simulation using a mathematical
body of spline functions is an efective means for a solution of
a wide scope of research problems in biolody, medicine and ecology.
Поляков Рудольф Валентинович,
1938 года рождения. В 1961 г. окончил механико-математический
факультет Днепропетровского госуниверситета, где до 1964 г.
был на преподавательской работе. С ноября 1964 г. - аспирант
Института математики АН УССР. Диссертацию защитил по математике
приближения функций комплексного переменного. С 1975 г. работает
в Институте физики национальной АН Украины (бывший ИФ АН УССР),
кандидат физико-математических наук, старший научный сотрудник
отдела теоретической физики. Автор 62 опубликованных научных работ.
Область научных интересов: теория приближения функций, приближенные
методы решения интегральных уравнений с использованием сплайн-функций,
разработка методов вычислительной физики и их применение к исследованию
нелинейных процессов в физических, экологических и биологических
системах.
Старков Вячеслав Николаевич, 1941 года рождения. Образование получил в Самарском аэрокосмическом университете (КуАИ), Санкт-Петербургском госуниверситете (ЛГУ) и аспирантуре Института математики НАН Украины.
Кандидат физико-математических наук, старший научный
сотрудник отдела теоретической физики Института физики НАН Украины.
Автор более 60 опубликованных научных работ. В 1986 г. участвовал
в ликвидации аварии на ЧАЭС. Область научных интересов: дифференциальные
и интегральные уравнения, сплайн-аппроксимация, вычислительная
физика, динамическая голография, нелинейная оптика, физика плазмы,
биофизика, экология, нейроинформатика.
Тивончук Василий Иванович, 1932 года рождения. В 1954 г. окончил физико-математический факультет Кременецкого (в наст. время Тернопольского) пединститута. С ноября 1961 г. обучался в аспирантуре Института математики АН УССР, диссертацию защитил по приближенным методам решения интегральных уравнений. С 1975 г. работает в Институте физики национальной АН Украины (бывший ИФ АН УССР), кандидат физико-математических наук, старший научный сотрудник отдела теоретической физики. Автор свыше 70 опубликованных научных работ. Область научных интересов: дифференциальные и интегральные методы высшего анализа и вычислительной физики и их применение к исследованию нелинейных процессов в физических, экологических и биологических системах.