СИСТЕМНАЯ ОРГАНИЗАЦИЯ
ПРОЦЕССОВ МЫШЛЕНИЯ: САМООРГАНИЗАЦИЯ И ФИЗИОЛОГИЯ ЧЕЛОВЕКА ПРИ ПРИНЯТИИ
УДОВЛЕТВОРИТЕЛЬНЫХ РЕШЕНИЙ*
Р. А. САДЫХОВ, Э. И. ВЛАДИМИРСКИЙ,
У. С. МАМЕДОВА**
1. Введение
Рассматривается открытая нечеткая метасистема
принятия удовлетворительных решений в условиях неравновесности, основой которой
являются самоорганизующиеся принципы кибернетики и нормальной физиологии
человека. В рамках предложенной метаситемы организация процессов мышления
представлена моделью хаотической нейронной сети и гибридной технологией
реализации целей отдельных функций метасистемы. Разработана
структура и математическая модель метасистемы принятия решения в условиях
неравновесности, нечеткости, а также предложена мера структурной устойчивости
каждой структуры вывода в отдельности и их комбинаций.
Рассмотрим концепцию эволюции биосферы акад.
Н. Н. Моисеева. Согласно
этой концепции биосфера в целом и ее различные подсистемы испытывают
воздействие извне и, реализуя возможности саморазвития, с одной стороны,
претерпевают изменения, а с другой - стремятся сохранить себя в неизменном
виде. Если стремление к неизменности
(гомеостатичность) доминирует и система не способна существенно или вообще
меняться, то "внешний" вызов может обусловить уничтожение системы
либо извне, либо от ее внутреннего перенапряжения. Если,
напротив, потенциал к неизменности превалирует, то способность к непрерывным
перестройкам может расшатать систему изнутри и также вызвать процесс ее
саморазрушения. Оптимальное сочетание устойчивости и
изменчивости, называемое пластичностью, обеспечивает развитие системы. Биосферу рассматривают как функцию, а устойчивость и
изменчивость - как аргументы. Рост разнообразия форм
зависит от того, каким образом сочетаются устойчивость и изменчивость. Если оба аргумента оптимально активны, то обеспечивается
широкое разнообразие форм, не переходящее определенных границ. Границы процесса Н.Н. Моисеев
назвал обозримыми каналами эволюции. Время от времени
эти границы исчезают, и тогда перед системой возникает возможность
неограниченного поиска нового канала эволюции. Момент
исчезновения границ и выбора дальнейшего пути развития называется бифуркацией,
или катастрофой. Момент бифуркации - это состояние
непредсказуемости, в отличие от движения в рамках канала эволюции. Лишь два основных принципа действуют не только во время
эволюции в канале с обозримыми границами, но и при бифуркации: принцип Онзагера и принцип Ле Шателье [1]. Первый можно
сформулировать как закон минимума диссипации, или минимума рассеяния энергии: в
соответствии с этим система выбирает тот переход, который обеспечивает
наименьшие затраты энергии. Данный принцип природы и
общества носит разные наименования (в экономике и политике - это так называемый
оптимальный выбор). Принцип фундаментален: любая
система - как обладающая, так и не обладающая разумом - сообразует с ним свои
действия.
Второй фундаментальный принцип также
прост: если на систему оказывается внешнее давление, то она сопротивляется,
осуществляя внутренние перестройки - структурную и функциональную.
Э.С. Кульпин
установил факт превалирования, или главенствующей роли неантагонистических
отношений в эволюции биосферы. Во взаимоотношениях
человека и природы в наши дни принцип неантагонистических отношений стал условием
сохранения рода человеческого, который назван "со-жизнь". Из триады (принципы Онзагера, Ле Шателье, "со-жизнь")
он является главным [1].
В процессе развития живой природы
выделяется род Homo,
ставший разумным и создавший свою автономную систему отношений - общество. С
течением времени эта система по сложности внутренней организации и силе
воздействия на природу поднялась до равенства с той системой, из которой она
выросла. Ввиду сложности этих систем воздействие их
друг на друга принимает многогранные формы, наиболее важные из которых имеют
тенденцию к прямой и обратной связям. Однако законы
биосферы и законы общества проявляются в социальной истории неравнозначно,
поэтому практически действуют лишь те из них, которые способны проявить себя во
временных, пространственных и системных границах. Естественно,
что кризис одновременно природы и общества - это социально-экологический
кризис. Поэтому способ существования общества и
природы в идеале должен быть таким, чтобы негативное воздействие природы на
общество и общества на природу было минимальным, не нарушающим
"устойчивости" и "стабильности" обеих систем [1].
Принцип "со-жизнь" отвечает
условиям адаптации в процессе взаимодействия элементов системы "человек -
природа".
Рассмотрим процессы взаимодействия системы
"человек - природа" - "решающая система" в контексте
исследования механизмов адаптации, устойчивости и в плане принятия решений при
неопределенности исходных данных.
Процесс принятия решений, удовлетворительных с точки зрения
пользователей, должен рассматриваться в рамках моделирования системной
организации мышления. Таким образом, мы подошли к
исследованию вопросов принятия решений в контексте взаимодействия Soft Computing-технологии и интегративной
физиологии человека, основу которой составляет теория функциональных систем,
предложенная академиком П. К. Анохиным [2].
2.
Система "человек - природа"
Система "человек - природа"
относится к классу открытых систем, функционирующих в дискомфортных, или
неравновесных состояниях. Неравновесные состояния
открытых систем конструктивны благодаря их способности к самоорганизации, то
есть к "пороговому" локальному самоупорядочению с образованием
диссипативных структур. Такое поведение - необходимый
элемент процесса рецепции информации, так как рецепция есть процесс
неравновесный [3]. Самоорганизация систем
демонстрирует роль хаоса как созидательного начала и конструктивного
нелинейного многовариантного механизма эволюции.
Класс систем, способных к
самоорганизации, - это открытые и нелинейные системы. Открытость
системы означает наличие в ней источников и стоков. Источники
и стоки имеют место в каждой точке таких систем. Открытость
системы - необходимое, но недостаточное условие для ее самоорганизации, т.е.
всякая самоорганизующаяся система открыта, но не всякая открытая система -
самоорганизующаяся и может создавать структуры.
Сложноорганизованные системы имеют тенденцию
распадаться, достигая своего развитого состояния. Устойчивость
вырастает в результате неустойчивости, ибо начало, т.е. рождение нового структурного
образования связано со случайностью, хаосом. Стадии
устойчивости и неустойчивости, оформления структур и их разрушения, сменяют
друг друга.
При определенных условиях, когда
работа источника интенсивнее диссипативного, размывающего неоднородности фактора,
устанавливается режим оформления структур в открытой нелинейной среде - LS-режим. Развитые
локализированные структуры неустойчивы к хаотическим флуктуациям на
микроуровне. Малые возмущения десинхронизируют темп
развития процессов внутри разных фрагментов сложной структуры, и она начинает
распадаться.
Процесс распада останавливается, если
вовремя (за счет хаоса, флуктуаций) происходит перескок на иной,
противоположный режим. Это - HC-режим, режим "неограниченно разбегающейся волны",
возобновления процессов по старым следам. Распад
(хотя бы частичный) заменяется объединением, максимальное развитие
неоднородностей - их размыванием.
Таким образом из хаотической массы
элементов строятся активно действующие функциональные системы. А это, в свою
очередь, характеризует адаптивность процессов, протекающих в системе.
Важнейшим состоянием синергетической системы
является хаос, или, точнее, хаотическая динамика. Самоорганизующаяся
система способна находить выходы из хаоса благодаря микропроцессам -
флуктуациям, разрастающимся в критических состояниях до макроразмеров. Поведение таких систем описывается нелинейными уравнениями,
имеющими два или более решений. Поэтому система, а
также еT отдельные участки, выходя из хаоса, выбирают в точках бифуркаций более
или менее случайно один из возможных путей стабильного развития с формированием
диссипативных структур, с повышением сложности структур и порядка.
Таким образом, методологическое
содержание синергетики способствует новому видению мира, формирует эволюционное
мышление.
3.
Подсистема "человек"
В. С. Степин
[4] выделяет три стадии, три системных состояния науки: первому состоянию -
классической науке - соответствует ньютоновская механика; второму -
неклассической науке - теория относительности и квантовая механика, третьему -
современному (постнеклассическому) - соответствует неравновесная термодинамика,
обобщенная до синергетики. Сфера синергетики
расширяется так, что ее методы могут быть использованы для анализа таких тонких
процессов, какими являются переходы от восприятия к мысли, от "хаоса к
порядку". Действительно, мозг здорового человека
(согласно исследованию его активности) представляет собой крайне неустойчивую,
хаотическую систему [3]. Выход из хаотических
состояний под влиянием окружения, по-видимому, сопровождается корреляцией
сенсорных стимулов и образованием упорядоченных когерентных структур.
Показано, что предельно неустойчивой
хаотической системой является мозг здорового бодрствующего человека [5]. В
качестве аналога хаоса в когнитивных процессах можно истолковать разнообразие
элементов знания, составляющих креативное поле поиска, наличие различных
сценариев движения в проблемном поле мысли [6]. Здесь
необходимо заметить, что разнообразие элементов знания, строго говоря, не
тождественно хаосу. Например, есть часть
неконструктивного, аналитически еще не обработанного знания. Кроме того, в процессе напряженного поиска с подключением
интуиции в сферу просматриваемого втягиваются элементы внесистемного знания,
образующие в сознании лишь слабые следы.
Что касается "вспышек
интуиции", то Е. Л. Файнберг [7] рассматривает
ее в двух аспектах: интуиция-суждение и интуиция-догадка, которые принадлежат к
разным сферам несознаваемого психического.
Интуиция-суждение есть результат деятельности
подсознания, где хранится ранее накопленный опыт. Здесь
нет творчества, нет новизны.
Иное дело - интуиция-догадка,
порождаемая неосознаваемым рекомбинированием ранее накопленного опыта, которое
побуждается и направляется доминирующей потребностью в поиске средств ее
удовлетворения, что, в свою очередь, означает, с синергетической точки зрения,
попадание в поле одного из креативных аттрактаров.
В соответствии с постулатами общей
теории функциональных систем процесс мышления динамически развертывается во
времени на основе последовательно сменяющих друг друга узловых стадий системной
организации целенаправленного акта: афферентного синтеза, принятия решения,
акцептора результата действия, эфферентного синтеза, действия и постоянной
оценки достигнутого результата с помощью обратной афферентации. На основе квантования психической деятельности строятся
процессы абстрагирования, которые определяют различные проявления мыслительного
процесса, начиная с различных проявлений интуиции, логических операций и кончая
творческой деятельностью [8].
Постоянная оценка достигнутого результата с
помощью обратной афферентации - аналог действия механизма обратной связи и,
естественно, адаптационных процессов в контексте принятия решения.
4. Хаос
и порядок в нелинейных диссипативных сферах
Хаос, его роль в познании строения и
эволюции мира весьма конструктивна. Как утверждают А.
В. Гапонов-Греков и М. И. Рабинович [9], "два понятия нелинейной физики -
стохастичность и структура... в действительности не являются антиподами. Хаос и порядок могут, в частности, непрерывно
трансформироваться друг в друга при изменении параметров системы. Не будет даже большим преувеличением сказать, что не бывает
ни абсолютного порядка, ни абсолютного хаоса - это лишь предельные ситуации. Всякая же реальная система пребывает в некотором
промежуточном состоянии, и оценивать следует близость этого состояния к одному
из предельных, то есть к абсолютному порядку или полному беспорядку".
В [10] отмечено, что "... если
мы конструируем структуру реального мира как переход хаос - порядок - хаос, то
таковой она и будет, и наши системы должны будут включать в себя огромные
управляющие устройства, способные создавать и поддерживать стадию порядка. Но если структуру бытия мыслить как переход "порядок -
хаос - порядок", то мы получим другое бытие, и наши системы станут в
значительной степени самоорганизующимися".
Анализ вышеизложенного позволяет с
принципиально новых позиций подойти к конструированию некоторой
интеллектуальной метасистемы принятия удовлетворительных решений в условиях
неопределенности исходной информации.
Большой интерес вызывает изучение
нелинейных диссипативных сред. При исследовании таких
сред было замечено, что в них часто происходит уменьшение числа степеней
свободы, эффективно описывающих систему. Они
определяют динамику процессов и поэтому часто называются параметрами порядка. При изучении диссипативных систем можно надеяться на их
упрощенное описание или же на построение целой иерархии упрощенных моделей. Уменьшение числа степеней свободы означает, что в системе
происходит самоорганизация. По определению [11],
самоорганизация - способность системы перестраивать свою внутреннюю структуру,
то есть у нее появляются свойства, которыми не обладает ни одна из подсистем. Теорию самоорганизации часто называют синергетикой. Г Хакен [12] поясняет это
следующим образом: "Я назвал новую дисциплину синергетикой. В ней
исследуется совместное действие многих подсистем (преимущественно одинаковых
или нескольких различных видов), в результате которого на макроскопическом
уровне возникает структура и соответствующее функционирование. С другой
стороны, для нахождения общих принципов, управляющих самоорганизующимися
системами, необходимо кооперирование многих различных дисциплин".
Возникновение структур, тесно связанных с
диссипативными процессами (диссипативные структуры), оказалось общим свойством
самых разных нелинейных систем. Г. Николис и И. Пригожин это понятие характеризуют так: "... как
удаленность от равновесия, так и нелинейность могут служить причиной
возникновения упорядоченности в системе. Между
упорядоченностью, устойчивостью и диссипацией возникает в высшей степени
нетривиальная связь, мы будем называть упорядоченные конфигурации, появляющиеся
вне области устойчивости термодинамической ветви, диссипативными структурами...
Такие структуры могут существовать вдали от
равновесия лишь за счет достаточно большого потока энергии и вещества... Диссипативные структуры являют собой поразительный пример,
демонстрирующий способность неравновесности служить источником
упорядоченности" [12].
В равновесных системах
диссипативные процессы уничтожают любую упорядоченность - устанавливается
термодинамическое равновесие. В нелинейных открытых системах диссипация
выступает в совершенно ином качестве - ее совместное действие с другими
процессами приводит к возникновению структур. Она
влияет на тип, форму и размеры. Основным аппаратом,
который используется при исследовании нелинейных сред, являются уравнения с
частными производными. Формально они описывают системы
с бесконечным числом степеней свободы. Однако не все
степени свободы играют одинаковую роль. В нелинейной диссипативной системе
обычно удается выделить конечное, а иногда и небольшое число переменных, к
которым "подстраиваются" все остальные. Эти
переменные обычно называют параметрами порядка.
В мозге все "высшие"
процессы, такие, как восприятие, речь, письмо, чтение и ощущение не могут
рассматриваться как изолированные друг от друга или "неделимые"
способности, являющиеся прямыми функциями ограниченной группы клеток или строго
локализованные в какой-то конкретной области мозга. Вместо
локализованных областей используются несколько каналов передачи информации
(афферентные пути), управление через обратную связь (обратная афферентация) и
процессы хранения информации и ее интеграции. Таким
образом, "интеллектуальные" функции рассматриваются как сложные
функциональные системы, организованные в когерентно работающие зоны, каждая из
которых может принадлежать совершенно различным и часто удаленным друг от друга
на достаточно большое расстояние областям мозга. Такие
группы определяют иерархический уровень, выполняющий каждый раз соответствующую
функцию.
В рамках макроскопического описания
активность каждой работающей зоны описывается ограниченным числом динамических
переменных, обычно координируемых процессами нелинейной обратной связи. Высшие иерархические уровни характеризуются возрастающей
долей участия церебральных тканей восходящего порядка и увеличивающейся
сложностью (от ствола головного мозга через ретикулярную формацию к коре
головного мозга). Последние уровни получили название
"когнитивных", и большинство из них в отличие от более низких,
"соматических", уровней формируются и разрушаются не только в ходе
эволюции, но также и в процессе обучения, происходящем за ограниченное время
жизни отдельного организма. Здесь следует иметь в
виду, что материальная "основа" всех этих высших когнитивных уровней
- нейроны. Один когнитивный уровень отличается от
другого числом, расположением и комбинацией, или схемой связи кооперирующихся
тканей. На каждом иерархическом уровне вводится
описание в терминах пространства состояний. Это
описание включает в себя тип и число динамических переменных и параметров, а
также получающиеся в результате тип и число состояний, соответствующие данному
уровню. Движение и поведение системы в этом фазовом
пространстве на фиксированном иерархическом уровне (например, последовательные
переходы из одного стационарного состояния в другое, "время покоя"
или свойства устойчивости каждого состояния, а также время между
последовательными стационарными состояниями) зависят от решения эволюционного
уравнения и от возмущаемых параметров системы, которые приводят к серии
переходов, связанных с ветвлением, или бифуркацией. Эти
возмущения являются результатом совместного влияния передачи информации
(афферентных сигналов), поступающей с ближайшего уровня снизу, информации,
поступающей от внешней среды (через периферическую нервную систему), и
управление через обратную связь (обратная афферентация), осуществляемая с
помощью сигналов, которые поступают с ближайшего уровня сверху. Естественно, что эти критические изменения приводят к
неустойчивости системы.
Так, например, на рассматриваемом
уровне Z система должна перейти в
другое стационарное состояние (или приспособиться к нему), задаваемое той же
системой связанных между собой нелинейных дифференциальных уравнений,
моделирующих систему на уровне Z с
новыми граничными условиями (например, с новыми значениями управляющих
параметров). Переходы с нарушением симметрии в
нелинейных сильно неравновесных системах получили название "диссипативные
структуры" (новые иерархические уровни) [13]. Там
же, с общих позиций, каждая иерархическая платформа рассматривается как
динамический элемент, где происходит "хранение и сбор" информации,
которые описывается с помощью кросс-корреляции, что ассоциативно подтверждается
корреляцией элементов в организме, при которой ткани под непрерывным
корригирующим влиянием результата деятельности функциональной системы
устанавливают равноправные взаимодействия. Так,
физиологическими веществами, участвующими в коррелятивных взаимодействиях
клеток, могут быть гормоны, медиаторы и др. [15]. Что
касается кросс-корреляции, то она означает, что сигналы 
, передаваемые последовательно с нижнего уровня и
сигналы 
, приходящие из внешней среды, усредняются (например,
по времени) после поступления на "принимающей платформе" У (например, на
определенном скоплении постсинаптических пластинок в коре головного мозга). В результате
этого некоторые из переменных 
полностью "вымываются" на верхнем уровне, в
то время как другие оказываются кросс-коррелированными, или спаренными:
(1)
где Т - временной интервал передачи
либо с нижнего уровня X, либо из
внешней среды. Отсюда напрашивается вывод, что между
событиями, происходящими одновременно на различных иерархических уровнях,
имеется скорее корреляционное, чем причинное соответствие [13]. Тогда система связанных нелинейных интегро-дифференциальных
уравнений для макроскопических динамических переменных 
, которые в отсутствие пространственной дифференциации
(
) имеют вид
,
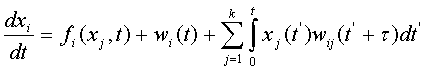(2)
где 
- нелинейные "скорости", заменяющие все
возможные связи между соответствующими переменными;
- флуктуации, индуцированные окружающей средой;
третий член уравнения - описывает
влияние оператора кросс-кореляции на иерархический уровень X.
Исследование этой системы связанных нелинейных
интегро-дифференциальных уравнений позволяет "выращивать" новые
иерархические уровни.
5.
Фрактальная размерность
Коэффициент "сжатия" (или подобия)
М. Фейнгенбаума [13] придает распределению
точек/состояний на интервале [0, 1] характер самоподобия.
Определение 1. Под самоподобием понимается свойство
объекта, структура которого наблюдается в одном масштабе, повторяться в
последовательно уменьшающихся масштабах. Рассматриваемая
фрактальная размерность имеет следующую природу. Так,
прямая в евклидовом пространстве имеет размерность 1. Следовательно,
для любого положительного целого N отрезок
0 ё x ё X может быть разложен на N
неперекрывающихся отрезков вида 
. (3)
Каждый из этих отрезков получается из
целого преобразования подобия
(4)
Аналогично, плоскость имеет размерность 2. Следовательно, для любого точного квадрата (числа) N прямоугольник
0 ё x ё X , 0 ё yё Y может быть разложен на N
неперекрывающихся прямоугольников вида: 
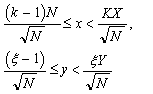(5)
(6)
где K и 
принимает значения от 1 до 
.
Каждая из этих частей получается из
целого преобразованием подобия с коэффициентом подобия 
. В общем случае, если 
- положительное число, то D-мерный прямоугольный параллелепипед может быть разложен на N параллелепипедов, каждый из которых
получается из исходного параллелепипеда преобразованием подобия с коэффициентом
подобия 
Таким образом, размерность D характеризуется соотношением [13]
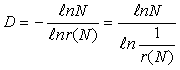(7)
Исходя из вышеизложенного и учитывая, что
модель памяти представляет собой иерархическую ассоциативную структуру,
например, дерево, то, представляя дерево в виде некоторой геометрической структуры,
можно определить ее фрактальную размерность.
В свете изучения аттракторов важно
отметить, что генерация ценной информации возможна, когда в динамической
системе имеется так называемый перемешивающийся слой [3].
Его особенность по сравнению с явлением
странного аттрактора состоит в том, что фазовые траектории с одной стороны
входят, а с другой - выходят из слоя. В фазовую область странного аттрактора
траектории только входят, но не выходят из нее, а запутываются внутри, поэтому
представление о странном аттракторе ассоциируется с квазистационарным
состоянием, но не со стянутым к одной точке, а размазанным по области фазового
пространства. Для понимания процесса генерации
информации важно учесть существование диссипативных систем, имеющих несколько простых
устойчивых состояний. Однако начальные состояния
задаются в такой области, что предсказать, в каком из этих состояний окажется
система, невозможно, ибо между начальным неустойчивым и конечным устойчивым
имеется перемешивающийся слой.
Таким образом, информационная система
должна обладать как устойчивым, так и неустойчивым состояниями. Обязательным является наличие перемешивающегося слоя, ибо
он стимулирует возникновение информации, которое происходит случайно,
независимо от начальных условий системы. В противном случае генерация
информации невозможна. Связь возможности генерации
информации с наличием устойчивых и неустойчивых состояний выдвигает задачу
оценки устойчивости на основе анализа динамических систем.
6. Устойчивость
биосистем
Классическая теория устойчивости в основном
изучает равновесные состояния систем и динамику их поведения в малой
окрестности этих состояний. Подобные классические
представления об устойчивости оказываются весьма плодотворными в физических и
технических приложениях. Что касается их применения к
анализу систем, изучаемых биологией, экономикой и общественными науками, то оно
должно быть достаточно взвешенным и конструктивным. Дело
в том, что обычный режим функционирования подобных систем, как правило, далек
от равновесного. Кроме того, внешние воздействия
постоянно изменяют само равновесное состояние. Постоянные
времени таких систем настолько велики, что во многих случаях ценность
классического анализа устойчивости очень мала.
Центральным элементом современных взглядов на
вопросы устойчивости является понятие структурной устойчивости [14]. Здесь основной задачей является выявление качественных
изменений в траектории движения при изменениях структуры самой системы. Таким образом, здесь изучается поведение данной системы по
отношению к поведению всех "близких" к ней аналогичных систем. Если рассматриваемая система ведет себя "почти так
же", как и "соседние", то говорят, что она структурно устойчива;
в противном случае - структурно неустойчива. Естественно
возникает вопрос, что такое близкая система, каков класс допустимых возмущений
и что означает схожесть поведения. Тем не менее,
основная идея остается прозрачной, достаточно малые изменения структурно
устойчивой системы должны приводить к соответственно малым изменениям в динамике
ее поведения. Что касается метаболизма организма, то
здесь необходимо обратить внимание на принцип саморегуляции. В самой общей
форме принцип саморегуляции был обнаружен И. П. Павловым при исследовании деятельности сердца и
кровообращения. В функциональных системах саморегуляция приобретает специальную
направленность. Так, отклонение от уровня,
обеспечивающего нормальной метаболизм (жизнедеятельность) организма и его
адаптацию к окружающей среде, является стимулом к мобилизации необходимых
элементов системы для обеспечения этого результата. Благодаря
динамической саморегуляторной деятельности системы организма определяют
необходимую для нормальной жизнедеятельности устойчивость метаболических
процессов и их динамическую уравновешенность с внешней средой. Так, в работе [15] постулируется, что "...всякое
отклонение от жизненно важного уровня какого-либо значимого физиологического
фактора служит причиной немедленной мобилизации многочисленных аппаратов
соответствующей функциональной системы, вновь восстанавливающих этот жизненно
приспособительный результат". При этом, как
отмечено в этой же работе, "... в нормальных условиях в деятельности
каждой функциональной системы проявляется следующая закономерность: общая сумма
механизмов, возвращающая отклоненный результат к исходному уровню, всегда
превышает сумму отклонений механизмов", то есть имеет место "запас
прочности", позволяющий ей справиться с любыми возможными отклоняющими
воздействиями. Известно, что "условием свободной
жизни организма является постоянство внутренней среды". Однако известно и то, что внутренняя среда организма
благодаря активным метаболическим процессам постоянно изменяется, и ее
отдельные показатели удерживаются около определенных значений только благодаря
консерватизму рецепторных образований и деятельности соответствующих
функциональных систем. Консерватизм рецепторов
является ограничителем пластичных изменений внутренних констант организма. Что касается восстановления оптимального для организма
уровня тех или иных показателей его внутренней среды, то здесь работают другие,
более пластичные, центральные и эффекторные механизмы деятельности
функциональных систем. Известно, что пластическими
свойствами в функциональных системах обладают эффекторные центральные и
периферические механизмы, и именно эти механизмы определяют взаимозаменяемость
и компенсацию в деятельности различных функциональных систем при выходе из
строя того или иного звена, органа или ткани. Однако
для функциональных систем многосвязного взаимодействия характерен качественно иной
принцип саморегуляции, и отклонение от оптимального уровня того или иного
параметра результата есть стимул к направленному перераспределению в
определенных соотношениях значений всех других параметров результата обобщенной
функциональной системы.
Выше было сказано, что пластичность
есть оптимальное соотношение между устойчивостью и изменчивостью системы. Ассоциируя этот тезис с пластичностью функциональных
систем, приходим к выводу: в обоих случаях системы стремятся к устойчивому
состоянию, только в первом случае - это процесс саморегуляции, а во втором -
процесс "обучения". И в том, и в другом
случае имеет место ассоциация с принципом неантагонистических отношений
"со-жизнь", что минимизирует возможность возникновения бифуркаций.
Таким образом, обращаясь к процессам
анализа системной организации мышления и учитывая, что режим функционирования
таких систем далек от равновесного, в работе предлагается оценивать соотношение
между устойчивостью и изменчивостью. Отсюда
структурная устойчивость будет характеризоваться мерой пластичности. Мера пластичности, в свою очередь, может в какой-то мере
характеризовать нарушение симметрии в процессе гистерезисного типа. В этой
связи приведем пример динамики перехода из состояния в состояние,
обусловленного не потерей устойчивости существующего состояния, а гистерезисом,
или пластической модификацией в системах, обладающих существенным стационарным
состоянием [16].
Пусть дана одномерная система X (например, линейный осциллятор с
сильным затуханием), описываемая дифференциальным уравнением 
. Очевидно, что эта система
обладает единственным ("симметричным") устойчивым стационарным
состоянием x=0. Пусть
эта система связана с "окружающей средой" У, также одномерной, единственная
переменная, у которой сдвигается управляющим параметром среды a следующим
образом: 
, где 
= const (или 0) при всех t, предшествующих интервалу
времени длиной 2Т, на котором
параметр a
"активируется", а затем снова падает до нуля. Считается,
что система X связана с окружающей
средой следующим способом, а именно: 
.
а) Интервал [
]: 
,
поэтому
(8)
,
(9)
где с - константа.
При t=T (середина интервала)
,
(10)
.
(11)
б) Интервал [
]: 
, (12)
поэтому
,
(13)
где k - константа, значение которой вычисляется
из условия, что величина 
при t=T должна быть равна Т2/2;
следовательно, k = - Т2 и
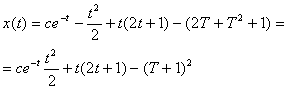(14)
Но тогда 
. (15)
В конце интервала 2Т: У(2Т) = Т2.
При t > 2T величина
У(2Т) остается неизменной. Таким образом, при t > 2T
поведение 
, которое всегда задается дифференциальным уравнением 
, описывается разновидностью последнего -
дифференциальным уравнением
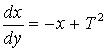(16)
и имеет устойчивое стационарное
состояние, отличное от предыдущего стационарного состояния. Задается
вопрос, как исчезло предыдущее стационарное состояние и уступило место новому?
В данном случае имеет место пример "пластического" изменения,
вызванного в системе X не потерей
устойчивости, приводящей к бифуркации, а переходным процессом, происходящим с
конечной "скоростью реакции". То есть в
системе X произошло стирание
стационарного состояния 
, а количество У=Т2
"реагирующего вещества" У оказалось записанным в системе, что рассматривается как
аналог "следа в памяти", оставленного в системе локальным отклонением
внешнего управляющего параметра от исходного значения. И
в этой ситуации, если не произошло изменения структуры, то мы имеем возможную
структурную устойчивость системы.
Проведенный на междисциплинарном уровне анализ
вышеизложенного позволил подойти к формированию комплексной проблемы реализации
нечеткой интеллектуальной метасистемы принятия решений, идеологической базой
которой является симбиоз Soft Computing-технологии и нормальной физиологии
человека. В контексте вышеизложенного имеет место следующая постановка задачи.
Пусть система "человек
- природа" 
-
открытая нечеткая система, функционирующая в неравновесных состояниях; пусть
подсистема "Человек" 
- нечеткая подсистема нечеткой системы 
, представляющая собой модель хаотической нейронной
сети; пусть "решающая система", 
- нечеткая интеллектуальная система, взаимодействующая
с нечеткой системой 
.
Тогда интеллектуальная система принятия
решений представляет собой открытую нечеткую метасистему, функционирующую в
неравновесных состояниях и имеющую вид
(17)
где " ~ " - обозначает нечеткость; 0 -
открытость; sub
- подсистема;* - операция взаимодействия.
В рамках выражения (18) ставится
задача реализации процесса принятия удовлетворительных решений в условиях
неравновесности и нечеткости исходных данных. Синергетика
изучает связь неустойчивости с так называемым динамическим хаосом. Имеет место связь: глобальная неустойчивость порождает
динамический хаос, который приводит в свою очередь к необратимости. Так, например, известно, что действительная реакция аксона
нейрона в мозге человека хаотична, если даже воздействие периодично. Реальные же отклики биологических нейронов на самом деле
более динамичные и сложные. В этом аспекте более чем корректно искать
адекватные модели нейронов с учетом нелинейности и хаотичности их поведения. Нам представляется, что наиболее удачно моделирование
процесса мышления может осуществиться с применением хаотических нейронных
сетей. Нейронные сети и хаос имеют общее характерное
свойство - нелинейность и непрерывность.
7. Структура
подсистемы "Человек"
Модель хаотического нейрона может быть
использована как составной элемент хаотических нейронных сетей при рассмотрении
пространственно-временной ситуации внешних входов и входов обратной связи от
других хаотических нейронов.
Таким образом, для целей моделирования
системной организации процессов мышления предлагается использование модели
хаотической нейронной сети, приведенной в [16]. Модель
нейронной сети включает обычные дискретные модели нейрона (типа
линейно-пороговой) и аналоговые нейроны с логистической функцией выхода. Следовательно, такая модель хаотической нейронной сети
является естественным расширением обычных дискретных нейронных сетей,
предусматривающих включение в эти модели хаотической динамики с целью
дальнейшего изучения детерминированного хаоса.
Рассмотренная модель хаотических нейронных сетей
позволяет генерировать различные динамические режимы, присущие сложным
нелинейным динамическим системам. Необходимо
заметить, что пространственно-временная динамика с прочностью саморекуррентных
тормозящих связей позволяет нейронным сетям действовать хаотично во фрактальной
структуре странного аттрактора в фазовом пространстве без застревания в
локальном минимуме.
8. Элементы
удовлетворительного принятия решений
Прогресс и перспектива Soft Computing-технологии,
представляющей собой комбинацию парадигм, таких, как нечеткая логика,
искусственные нейронные сети, эволюционное программирование, теория хаоса и
обучения предопределили и катализировали процессы экстенсивного развития теории
и техники искусственного интеллекта (ИИ).
Наряду с методами, составляющими базу Soft Computing-технологии представляет интерес
использование теории принятия удовлетворительных решений, что еще больше
расширяет ее возможности при реализации задач ИИ.
Основными сложностями при реализации этих
задач явились вопросы, связанные с анализом сходимости полученных решений. Введение таких фундаментальных понятий, как расширенные
топологические пространства, расширенные фильтры [18], принципиально
отличающиеся от классических, позволили решать вопросы сходимости в контексте
теории удовлетворительности, что выгодно отличается от методов оптимизации в
топологических пространствах.
Важным шагом вперед явилось расширение
этого подхода до высот использования аксиоматики нечетких множеств, что в
некоторой степени предопределило новые возможности теории удовлетворительности.
Герберт Саймон ввел термин
"удовлетворительность", ссылаясь на методы выбора, которые дают
хорошие результаты или удовлетворительные решения в отличие от оптимальных.
Саймон впервые связал сложность
человеческих ощущений с многообразием пространства. Более
того, Саймон развил множество своих идей, связанных с
удовлетворительностью "искусственных" систем. То
есть систем, имеющих заданную форму и ощущаемых только потому, что они отражают
те цели или устремления в их пространстве. Принцип
удовлетворительности решений является одним из самых простых принципов решения,
который принимается за рациональный. Этот принцип
является типичным принципом параметрического решения с функцией генерации
неопределенной оценки. Фундаментальная функция принятия решения должна определить, как будет
использована функция результирующего решения для выбора решения. Необходимо отметить, что принципы решения должны
классифицироваться в соответствии с их более точными структурами [19].
Однако в реальных условиях, в системах ИИ, не всегда имеют место точные структуры, да и в этом
наверное нет необходимости, так как точность может и не гарантировать
удовлетворительность.
Использование аксиоматики расширенных фильтров
может успешно решать поставленные задачи в контексте удовлетворения сходимости
полученных решений. Так, Хаммер
[20] определил фильтр как "любое устройство, которое принимает или
пропускает определенные элементы в системе и отвергает другие... Это определение совместимо с общепринятой языковой
концепцией и является широким обобщением топологического определения". Например, отношение удовлетворения является фильтром в том
смысле, что по этому отношению пропускаются или принимаются определенные
действия и отвергаются другие действия. То есть такая
перспектива открывает широкие возможности, и фильтры становятся унифицированной
концепцией для математиков. Так, функции являются фильтрами, уравнения - фильтрами,
отношения - фильтрами, система аксиом - фильтрами, определения - фильтрами и т.
д. Поэтому одна задача заключается в более конкретном
определении класса фильтров, а другая - в уточнении возможностей
"фильтрации".
Таким образом, в контексте принятия
удовлетворительных решений, на заключительном этапе функционирования
метасистемы использованы предложенные в [21- 23] аксиоматические аспекты
элементов расширенной топологии, позволяющие осуществить выбор в нечетких
монотонных и немонотонных пространствах. Использование
такого подхода при диагностике, профилактике и назначениях, практикуемых в
лечебной практике, дает возможность более корректно и со значительной
эффективностью осуществлять вышеуказанные мероприятия.
Литература
1. Кульпин Э. С.
// Восток, 1994.- N 1.- С. 29- 38.
2. Судаков К. В. Системное построение функций
человека.- Москва: "Sovero
Press", 1998.- 24 с.
3. Мелик-Гайказян И. В. Информационные процессы и реальность.- М.: Наука, 1998.- 192 с.
4. Юдин
Б. Г., Степин В. С. // Вопросы филосфии, 1994.- N 5.- С.155- 157.
5. Пригожин И. Р., Стенгерс И. Время, хаос, квант.- М.: Прогресс, 1984.- 272 с.
6. Князева Е. Н., Курдюмов С. П. Интуиция как самодостраивание // Вопросы
филосфии, 1994.- N 2.- С.110- 122.
7. Симонов П. В., Романовская Т. Б.. Файнберг Е. Л. // Вопросы филосфии,
1994.- N 1.- С.154- 158.
8. Судаков К. В., Агаян Г.
Ц., Вагин Ю. Е. И др. Системокванты физиологических процессов.- М.: 1997.- 152 с.
9. Гапонов-Греков А. В., Рабинович
М. И. Нелинейная
физика. Стохастичность и структуры // "Физика XX века. Развитие и
перспективы."
10. Сачков Ю. В. // Вопросы философии, 1994.- N 4.
- С.176- 182.
11. Першиков В. И.. Савинков В.
М. Толковый словарь по информатике.- М.: Финансы и статистика, 1991.- 543 с.
12. Ахромеева Т. С., Курдюмов
С. П., Малинецкий Г. Г., Самарский А. А. Нестационарные структуры и диффузионный хаос.- М.:
Наука,1992.- 544 с.
13. Николис Дж. Динамика
иерархических систем. Эволюционное представление.-
М.: Мир, 1989.- 488 с.
14. Касти Дж. Большие
системы: связность, сложность и катастрофы.- Мир,
1982.- 216 с.
15. Нормальная
физиология: Курс физиологии функциональных систем / Под ред. К. В. Судакова.- М.: Медицинское информационное агенство, 1999.- 718 с.
16. Алиев Р. А., Алиев Р.Р.
Soft Computing / Учебное пособие для вузов по специальности "Автоматизированные системы обработки информации и
управления". Ч.III. Гибридные
интеллектуальные системы.- Баку: АГНА,
1977.- 349 с.
17. Ю. А. Абилов, Р.
А. Алиев, И. М. Насиров. // Изв. АН: Теория и системы управления.-
1997, N 5.- C. 96- 99.
18. Robert F. Erlandson. The satisfacting Procces: A New Look IEEE Transaction on Systems, Man and
Cybernetics // SMC.- 1981, P. 740- 752.
19. Kyoichi Kiima and Yasihiko Takahara. Structural properties of the satisfactory
decision prinsiple // Jnt.
J. Systems Sci.- 1984.- Vol. 15, N 12.- Р.1323- 1339.
20. Мамедова У. С. Нечеткие фильтры в принятии решений // Материалы межд. конфер. "Логико-математические методы в технике, экономике и социологии".- Россия, Пенза.- 1998.- С. 35- 38.
21. Мамедова У. C. Принятие удовлетворительных решений в диагностических системах // Ученые записки.- Баку: АзТу, 1998.- Т. VII.- N 3.- С. 191- 196.
22. Мамедова У. C. Экспертно-диагностическая система // Материалы республиканской Научной конференции аспирантов и молодых ученых.- Баку, 1999.- Т 1. - С. 169- 170.
23. Мамедова У. C. Математическая модель принятия решений в диагностических системах // Ученые записки. - Баку: АзТу, 1999.- Т. VII, N 1.- С. 63- 66.
SYSTEMIC
ORGANIZATION OF MENTATION: SELFFORGANIZATION AND PHYSIOLOGY OF A HUMAN BEING IN
COMING TO AN ADEQUATE DECISION
R. A.
SADYKHOV, E. I. VLADIMIRRSKIY,
Summary
In the context of satisfactory decision-making the
authors suggest axiomatic aspects of extended-topology unit-cells for decision-making
in unclear-cut monotone spaces at a final stage of metasystem
functioning.