МОДЕЛИРОВАНИЕ СТРУКТУРНЫМИ УРАВНЕНИЯМИ
МЕЖСИСТЕМНЫХ И ВНУТРИСИСТЕМНЫХ СВЯЗЕЙ СКРЫТЫХ И ЯВНЫХ МОРФО-ФУНКЦИОНАЛЬНЫХ
ХАРАКТЕРИСТИК СЕРДЕЧНО-СОСУДИСТОЙ СИСТЕМЫ БОЛЬНЫХ АРТЕРИАЛЬНОЙ ГИПЕРТОНИЕЙ
С. В. Поветкин*
1. Введение
До настоящего времени
остается актуальной проблема изучения взаимосвязи и взаимообусловленности
адаптивных и дизадаптивных процессов, возникающих в сердечно-сосудистой системе
у больных артериальной гипертонией (АГ). Активно исследуются структурные и
функциональные изменения в сердце, сосудах, зависимость их от гемодинамических,
нейрогуморальных и других факторов, влияние системной гипертензии на
гемодинамику малого круга кровообращения [1-7]. Однако выполнение единого
комплексного исследования, оценивающего роль и место всех патогенетических
факторов, участвующих в дизадаптивной трансформации системы кровообращения у
больных АГ, представляется крайне сложным. Для изучения взаимосвязей
исследуемых морфо-функциональных показателей сердца с факторами, не вошедшими в
спектр определяемых параметров, но вносящими реальный вклад в формирование
адаптивных и дизадаптивных процессов в сердечно-сосудистой системе, широко
используются методы математического моделирования [8].
Целью работы являлась
оценка причинных связей между явными (изучавшимися) и скрытыми (не
изучавшимися) параметрами сердечно-сосудистой и других систем с помощью метода
моделирования структурными уравнениями.
2. Материалы и методы
Построение моделей,
оценивающих значимость и адекватность связей явных и скрытых факторов, участвующих
в реализации процесса сердечно-сосудистой дизадаптации у больных АГ, проводили
с помощью модуля SEPATH (selection of structural equation modeling techniques) программы STATISTICA v. 5.0.
Предварительное построение гипотетических
связей явных и скрытых факторов выполнялось на основе данных корреляционного
анализа, проведенного в группе, включавшей 276 пациентов с мягкой, умеренной и
тяжелой АГ. Средний возраст пациентов составил 49,4¦7,20
лет, средняя длительность заболевания 11,1¦4,90 лет. Показатели
морфо-функциональной структуры, диастолической функции левого желудочка,
гемодинамики малого круга кровообращения определяли на ультразвуковом сканере Aloka SSD-2000 и SSD-630 (Япония) с расчетом традиционных
параметров [9-12].
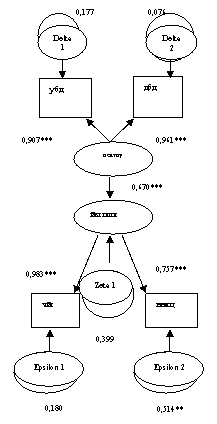
Рис. 1. Двухфакторная модель, оценивающая связи скрытых и явных
переменных.
Примечание: здесь и на рис. 2, 3:
прямоугольники - явные переменные; эллипсы - скрытые переменные; стрелки -
прямые связи (пути) между переменными; дуги - непрямые связи, оценивающие
дисперсии переменных в качестве свободных параметров; цифры - весовые значения
оценки прямых и непрямых связей; звездочки - степень достоверности весовых
значений связей.
При
создании структурных моделей руководствовались принципом описания скрытых
факторов, их взаимосвязей с минимально достаточным числом репрезентативных
явных параметров для получения должных или близких к ним значений критериев
адекватности модели.
В качестве скрытого
экзогенного фактора рассматривали нейрогуморальные системы регуляции
артериального давления (АД) и органные механизмы, потенцирующие процессы
ремоделирования сердечно-сосудистой системы (условное название
"НЕЙРОС"). В
качестве эндогенных скрытых факторов были рассмотрены аутокринные и паракринные
механизмы, обеспечивающие структурную перестройку морфологических единиц
сердечно-сосудистой системы и собственно дизадаптивные процессы, происходящие в
сердце и системе малого круга кровообращения (условные обозначения
"ФИБРОКОР" и "ПУЛЬМО" соответственно). Ошибки скрытых
эндогенных факторов имели имена Zeta 1 для
"ФИБРОКОР" и Zeta 2 для
"ПУЛЬМО". Явными
экзогенными переменными служили систолическое АД (САД) и диастолическое АД (ДАД). Оценивались также соответствующие остаточные
переменные Delta 1 и Delta 2. Эндогенными явными параметрами были
время изометрического расслабления (ВИР) левого желудочка (ЛЖ), масса миокарда
ЛЖ (ММЛЖ), размер левого предсердия (ЛП), систолическое давление в легочной
артерии (СДЛА). Им соответствовали остатки с именами Epsilon1, Epsilon2, Epsilon3, Epsilon 4.
Установочные параметры
анализа структурных моделей были следующие: использовали исходные данные с
последующим преобразованием их в корреляционную матрицу, над которой
проводились дальнейшие расчеты; оценка неизвестных факторов проводилась методом
наименьших квадратов с последующим применением метода максимального
правдоподобия; использовался метод кубической интерполяции в процедуре поиска
экстремума, завершенность которого оценивалась по достижению уровня значимости,
равного 0,0001; оценивались программой в качестве свободных параметров пути
между экзогенными, эндогенными переменными; дисперсии остаточных переменных и
ошибок скрытых эндогенных факторов; пути, связывающие остаточные переменные с
соответствующими им явными, а ошибки - со скрытыми эндогенными факторами, имели
фиксированное весовое значение, равное 1,0.
Для оценки адекватности
построенных моделей использовали следующие показатели: критерий
Брауна (MRC), который характеризует успешную
сходимость процедуры оценивания модели при его значении равном нулю; критерии
инвариантности модели (ICSF и ICS) должны иметь
значения, близкие к нулю; критерий граничных значений (BC), равный
нулю, свидетельствует об успешной сходимости процедуры оценивания модели;
индекс Стейгера - Линда (RMSEA) характеризует качественную подгонку модели при его
значении равном нулю; индекс нецентральности Мак-Доналдса
(MDIN) и индекс Джорескога
(GFI) характеризуют адекватность
построенной модели при значениях более 0,95; индекс стандартизованных остатков
(RMSSR) говорит о
хорошем качестве подгонки модели при значении менее 0,05; стандартизованные
остатки переменных. Их значения, равные или близкие к нулю, говорят об
адекватности модели.
3. Результаты
При
проведении моделирования структурными уравнениями использовали принцип ступенчатого
усложнения модели. В начале оценивалась базовая модель, описывающая зависимость
между "НЕЙРОС" и "ФИБРОКОР" на основе их связей с
соответствующими явными параметрами - АД, ММЛЖ, ВИР (рис. 1). Правильность
выдвинутых предположений о взаимосвязях подтверждалась оптимальным уровнем
критериев, оценивающих адекватность базовой модели (табл. 1, 2). Тестируемые
пути между скрытыми и явными переменными обнаружили существенные весовые
значения, подчеркивающие влияние "НЕЙРОС" на АД, "ФИБРОКОР"
на ВИР и ММЛЖ, а также подчиненность "ФИБРОКОР" по отношению к
"НЕЙРОС".
Таблица 1
Критерии адекватности базовой модели структурных
Уравнений
|
Критерии адекватности модели |
Значения
критериев
|
MRC
|
0,000000519 |
|
ICSF |
0,00000000824 |
|
ICS |
0,00000000443 |
|
BC |
0 |
|
RMSEA |
0 |
|
MDIN |
1,0 |
|
GFI |
1,0 |
|
RMSSR |
0,000733 |
Таблица 2
Стандартизованные остатки переменных
базовой модели структурных уравнений
|
Переменные |
ВИР
|
ДАД
|
ММЛЖ
|
|
САД |
0,000560 |
0,000000 |
-0,002072 |
|
ММЛЖ |
0,000000 |
0,000847 |
|
|
ДАД |
-0,000229 |
|
|
Таблица 3
Критерии адекватности промежуточной модели структурных уравнений
|
Критерии адекватности модели |
Значения
критериев
|
MRC
|
0,0000039 |
|
ICSF |
0,0000000141 |
|
ICS |
0,0000000136 |
|
BC |
0 |
|
RMSEA |
0 |
|
MDIN |
1,0 |
|
GFI |
1,0 |
RMSSR
|
0,000733 |
Следующим
шагом в усложнении модели была оценка влияния гипертрофического ремоделирования
сердца на процесс расслабления ЛЖ, что тестировалось включением в модель пути, связывающим
ММЛЖ с ВИР.
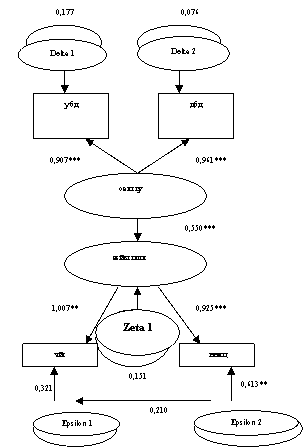
Рис. 2. Двухфакторная
модель, оценивающая связи скрытых и явных переменных, взаимосвязь между явными
эндогенными переменными
Измененная
модель (рис. 2) характеризовалась критериями адекватности (табл. 3, 4), близкими
к таковым базовой модели и некоторым изменением весовых значений путей,
оцененных программой. Полученные результаты свидетельствовали о том, что
предположение о взаимосвязях между скрытыми факторами, явными переменными
являлось правомерным.
Третьим
этапом трансформации модели было создание структурных уравнений, связывающих
все переменные, включенные в перечень анализируемых параметров. Рис. 3 отражает
вариант окончательной модели из числа построенных и подвергнутых тестированию.
Критерии адекватности итоговой модели соответствовали требуемому уровню (табл.
5, 6).
Построенная система структурных уравнений позволила в первую очередь оценить
параметры регрессионной модели, связывающей скрытые, не изучавшиеся в работе
факторы ("НЕЙРОС", "ФИБРОКОР", "ПУЛЬМО"),
лежащие в основе развития дизадаптивных процессов в сердце, малом круге
кровообращения, приводящих в конечном итоге к изменению явных, исследованных
морфо-функциональных параметров системы кровообращения у больных АГ. Весовое значение пути между "НЕЙРОС" и "ФИБРОКОР" составило 0,729 (р<0,001), "НЕЙРОС" и "ПУЛЬМО" равно 5,772 (р<0,001), "ФИБРОКОР" и
"ПУЛЬМО" оценено как -3,775 (р>0,05).
Таблица 4
Стандартизованные остатки переменных промежуточной модели структурных
уравнений
|
Переменные |
ВИР
|
ДАД
|
ММЛЖ
|
|
САД |
0,000560 |
0,000000 |
-0,00207 |
|
ММЛЖ |
0,000000 |
0,000847 |
|
|
ДАД |
-0,000229 |
|
|
Таблица 5
Критерии адекватности итоговой модели структурных
уравнений
|
Критерии адекватности модели |
Значения
критериев
|
MRC
|
0,0000012 |
|
ICSF |
0,00000000275 |
|
ICS |
0,00000000992 |
|
BC |
0 |
|
RMSEA |
0 |
|
MDIN |
1,0 |
|
GFI |
1,0 |
|
RMSSR |
0,000782 |
Таблица 6
Стандартизованные остатки переменных
итоговой модели структурных уравнений
|
|
|
ММЛЖ
|
ЛП
|
СДЛА
|
ДАД
|
|
САД |
0,000560 |
-0,002072 |
-0,000636 |
-0,000080 |
0,000 |
|
ДАД |
-0,000229 |
0,000847 |
0,000260 |
0,000033 |
|
|
СДЛА |
0,000130 |
-0,000481 |
-0,000230 |
|
|
|
ЛП |
0,000581 |
-0,002149 |
|
||
|
ММЛЖ |
0,000000 |
|
|||

Следует отметить, что оценки дисперсий ошибок "ФИБРОКОР" и
"ПУЛЬМО" близки к нулю. Минимальны также дисперсии остаточных переменных САД и ДАД. Связи самих уровней АД с "НЕЙРОС" во всех трех моделях сохранялись устойчивыми и достоверными. Подтверждена существенная роль факторов, входящих в переменную "ФИБРОКОР", в детерминации изменений параметров (ММЛЖ, ЛП, ВИР), отражающих структурную и функциональную дизадаптацию левых отделов сердца у больных АГ.
Несколько меньшими были весовые значения путей, связывающих САД, ДАД, ВИР, ММЛЖ с ЛП. Как органные скрытые факторы, так и явные экзогенные и эндогенные параметры в совокупности с локальными факторами, кодированными в переменной "ПУЛЬМО", опосредовали трансформацию легочной гемодинамики у пациентов с артериальной гипертонией, что проявлялось изменением уровня СДЛА.
Вышеизложенное свидетельствует о минимизации ошибочных предположений о связях скрытых факторов с явными переменными и влиянии этих факторов на дизадаптивные изменения морфо-функциональных параметров сердечно-сосудистой системы больных АГ.
4. Заключение
Таким образом, построенная с помощью структурных уравнений модель, основанная на оценке связей изученных морфо-функциональных параметров системы кровообращения с гипотетическими патогенетическими факторами органной дизадаптации, позволила обобщить на межсистемном уровне характер и направленность кардиоваскулярного ремоделирования у больных АГ.
Использование моделирования структурными уравнениями является адекватным методом оценки взаимосвязи явных и скрытых параметров биологических систем.
Литература
1. Алехин М.Н., Седов В.П. // Тер.арх.-
1996.- N 9.- С. 23-26.
2. Гургенян С.В., Адамян К.Г., Крищян
Э.М. // Кардиология.- 1996.- N 7.- С. 46-51.
3. Павлюкова Е.Н., Пузырев К.В., Цымбалюк Е.В., Карпов Р.С. // Клиническая
медицина.- 1999.- N 10.- С. 42-45.
4. Рязанов А.С., Смирнова М.Д., Юренев А.П.
// Тер. архив.- 2000.- N 2.- С. 72-77.
5. Стрюк Р.И., Длусская И.Г., Токмачев
Ю.К. // Кардиология.- 1996.- N 7.- С.42-45.
6. Темиров А.А., Катюхин В.Н. //
Кардиология.- 1987.- N 8.- C. 52-56.
7. Шляхто Е.В., Конради А.С., Захаров Л.В., Рудоманов О.Г. //
Кардиология.- 1999.- N 2.- С. 49-55.
8. Боровиков В.П., Боровиков И.П. Статистический анализ и обработка
данных в среде Windows.- М., 1997.- 592с.
9. Алехин М.Н., Седов В.Н. //
Тер. Архив.- 1996.- N 12.- С. 84-88.
10. Isobe M., Yazaki Y., Takaku F. et al. // Amer. J. Cardiol.-1986.- Vol. 57, N 4.- P. 316-321.
11. Schiller N.B. //
Hypertension.- 1987.- N 9.- Р. 33-38.
12.
Schiller N.B. // Circulation.- 1991.-
N 84. Р. 280-286.
Simulation of Intersystem and Intrasystem
Connections of Latent and
Obvious Morphological and Functional
Characteristics of a Cardiovascular System
in Patients with Arterial Hypertonia, Using
Structural Equations
S. V. Povetkin
Summary
The capability of an estimation of interconnection
between obvious (determined) morphological and functional parameters of a
cardiovascular system in patients having arterial hypertonia
with a series of the latent factors (not studied in activity) was studied by a
method of simulation by structural equations, that substantial by contributed
to formation of adaptive and disadaptative processes
in a system of blood circulation.
It was substantiated the capability of construction of
the adequate model grounded on an estimation of connections of studied
morphological and functional parameters of blood circulation with the
hypothetical pathogenetic factors of an organic disadaptation using structural equations, that permitted to
generalize the nature and directivity of cardiovascular remodeling in patients
with arterial hypertonia at an intersystem level.
Key words: disadaptative processes, arterial hypertonia