ИСПОЛЬЗОВАНИЕ НЕЙРОННЫХ СЕТЕЙ ДЛЯ ВЫДЕЛЕНИЯ
ИНФОРМАТИВНЫХ ПРИЗНАКОВ В ДИФФЕРЕНЦИАЛЬНОЙ ДИАГНОСТИКЕ СЕРДЕЧНО-СОСУДИСТЫХ
ЗАБОЛЕВАНИЙ
А.И. АБАКУМОВ*, Т.П. НОВГОРОДЦЕВА**,
Л.В. СОРОКИНА***
Многочисленными
медико-биологическими исследованиями доказана информативная и диагностическая
значимость показателей жирных кислот (ЖК) липидов крови при сердечно-сосудистых
заболеваниях (ССЗ) [1-7]. В указанных работах вопросы ассоциированности
ССЗ с модификацией состава ЖК в основном рассматриваются с точки зрения частоты
выявления и распространенности их нарушений в изучаемой популяции. В
отечественной и зарубежной литературе отсутствуют работы, в которых
используется сложный математический аппарат для подтверждения роли ЖК в
развитии заболеваний, установленной медико-биологическими исследованиями.
Дополнительные диагностические возможности показателей ЖК открывает специальная
математическая обработка, позволяющая установить взаимосвязь их отдельных
представителей со степенью патологических проявлений ССЗ. Широкое
распространение в медицине и биологии приобретают нейросетевые
технологии, идеальным полем применения которых
являются задачи классификации, позволяющие определить принадлежность объекта к
одному из нескольких возможных классов. При этом для принятия решений могут
использоваться самые разнообразные клинические, функциональные данные и
лабораторные тесты. Подобные классификации способствуют созданию систем для
диагностики и дифференциальной диагностики заболеваний. Цель настоящей работы -
использование нейронных сетей при
классификации ССЗ по показателям ЖК липидов эритроцитов крови для определения
их информативности в дифференциальной диагностике.
База данных проектировалась и анализировалась в НИИ
медицинской климатологии и восстановительного лечения СО РАМН (НИИ МКВЛ) и
включала итоги клинического и биохимического обследования 128 человек.
Обследуемые - жители юга Приморья старше 17 лет, русской национальности, обоего
пола, проживающие в данной климатической зоне более 10 лет. Обследуемые
на основании клинических симптомов были разбиты на 5 групп по степени
патологических изменений: группа здоровых, составившая 26 человек, без факторов
риска и клинических симптомов кардиальной патологии (КП); группа условно здоровых
(15 чел.) с отягощенной наследственностью по КП, но без клинических симптомов
заболевания; группа лиц с функциональными расстройствами в виде
нейроциркуляторной дистонии (НЦД) (30 человек);
группа больных с артериальной гипертонией (АГ) I, II, III ст. тяжести - 17
человек; группа больных ишемической болезнью сердца (ИБС) - 40 человек со
стенокардией 1-2 функционального класса, а также перенесшие инфаркт миокарда.
Нейронные сети
представляют собой нелинейные системы.
Искусственная нейронная сеть
(ИНС) - это набор нейронов,
соединенных между собой. Как правило, передаточные функции всех нейронов в сети
фиксированы, а веса являются параметрами сети и могут изменяться. Некоторые
входы нейронов помечены как внешние входы сети, а ряд выходов - как внешние
выходы сети. Подавая любые числа на входы сети, получаем какой-то набор чисел
на выходах. Т.о., работа нейросети состоит в преобразовании
входного вектора в выходной вектор, причем это преобразование задается весами
сети [9]. Каждый нейрон характеризуется своим текущим состоянием по аналогии с
нервными клетками головного мозга, которые могут быть возбуждены или
заторможены. Он обладает группой синапсов - однонаправленных входных связей,
соединенных с выходами др. нейронов, а также имеет аксон - выходную связь
данного нейрона, с которой сигнал (возбуждения или торможения) поступает на
синапсы следующих нейронов. Процесс функционирования ИНС, т.е. сущность
действий, которые она способна выполнять, зависит от величин синаптических связей, поэтому, задавшись определенной
структурой нейронной сети, надо найти оптимальные значения всех переменных
весовых коэффициентов. Этот этап называется обучением ИНС. Нейронные сети
отлично зарекомендовали себя при построении прогнозов, диагностике, принятии
решений, в предсказаниях и при решении др. задач классификации, для которых
важным является распознавание образов, а точные в числовом выражении ответы не требуются. Для изучения возможностей
применения нейронных сетей в определении
информативности показателей ЖК было обучено 3 нейронных сети различной
архитектуры. Использовался пакет NeuroShell
2 фирмы Ward Systems Group, Inc
[9].
Первая - нейронная сеть, построенная на
архитектуре многослойного персептрона с прямыми связями между нейронами и
алгоритма обратного распространения ошибки (стандартная сеть). Параметры сети,
обеспечившие ее обучение, следующие: количество
скрытых слоев равно 1, уровень точности выхода нейронов сети 0.01, скорость
обучения - 0.1, начальный вес - 0.3, передаточная функция - логистическая,
имеющая вид [9]:
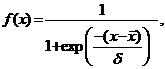
где`` x - означает среднее по всем значениям этой переменной в
файле данных, а d -стандартное отклонение
этих значений.
Число нейронов во
входном слое - 39, в выходном - 5, число скрытых нейронов для 3-слойной сети
(31) вычислялось по следующей формуле
[9]:
![]()
где Nhn - количество скрытых
нейронов, Ni
- число признаков, по которым
строится сеть, No
- число выходов в сети, Ne - количество примеров. Результаты работы
сети - в табл. 1.
Таблица 1
Результаты работы стандартной сети
|
|
Группы |
||||
|
I |
II |
III |
IV |
V |
|
|
R2: |
0,9772 |
0,5303 |
0,7520 |
0,8058 |
0,8937 |
|
Средняя квадратичная
ошибка: |
0,004 |
0,046 |
0,051 |
0,032 |
0,016 |
|
Средняя абсолютная ошибка: |
0,033 |
0,091 |
0,103 |
0,064 |
0,060 |
|
Мин. абсолютная ошибка: |
0 |
0 |
0 |
0 |
0 |
|
Макс. абсолютная ошибка: |
0,260 |
1,000 |
1,000 |
1,000 |
0,728 |
|
Коэффициент корреляции r: |
0,9908 |
0,7311 |
0,8690 |
0,8981 |
0,9495 |
|
Доля с ошибкой менее 5%: |
18,644 |
0 |
11,017 |
10,169 |
10,169 |
|
Доля с ошибкой от 5% до
10%: |
0 |
1,695 |
11,017 |
5,085 |
3,390 |
|
Доля с ошибкой от 10% до
20%: |
1,695 |
3,390 |
2,542 |
1,695 |
3,390 |
|
Доля с ошибкой от 20% до
30%: |
0,847 |
2,542 |
0,847 |
0,847 |
0 |
|
Доля с ошибкой свыше 30%: |
0 |
3,390 |
3,390 |
3,390 |
0,847 |
Как видно из табл. 1, наиболее правильно классифицированы
обследуемые из 1-й и 5-й группы (коэффициент корреляции 0,99 и 0,95
соответственно, т.е. ни один человек не был распознан как субъект из другой
группы).
Вторая сеть - нейронная сеть с общей регрессией (НСОР),
известная своей способностью к быстрому обучению на рыхлых наборах данных. При
тестировании обнаружено, что НСОР на многих типах задач (но не на всех) ведут
себя лучше, чем сети с обратным распространением ошибки [9]. Сети НСОР были
изобретены д-ром Дональдом Шпехтом [8]. НСОР представляет собой 3-слойную сеть (рис.
1), в которой должно быть по одному скрытому нейрону для каждого тренировочного
примера. В данной сети отсутствуют такие параметры тренировки, как скорость
обучения и момент, характерные для сетей с обратным распространением ошибки, но
имеется параметр сглаживания, использующийся после
того, как сеть натренирована. Этот параметр означает менее точное приближение
данных поверхностью при высоких значениях. Здесь он равен 0,3. Число нейронов
во входном слое (блок 1) равно числу входов в задаче (39), а число нейронов в
выходном слое (блок 3) соответствует числу выходов - 5. Число нейронов в
скрытом слое устанавливается автоматически и равно числу примеров в тренировочном
наборе.
Результаты работы
сети представлены в табл. 2: коэффициенты корреляции практически во всех
группах равны 0,99, за исключением 2-й группы, где коэффициент 0,95
свидетельствует о том, что сеть данной архитектуры наиболее точно классифицировала
субъектов по группам.
![]()
Рис. 1. Архитектура сети НСОР
Третья - сеть Ворда,
представляющая собой сеть с обратным распространением ошибки, в которую
добавлен третий блок в скрытый слой. Все блоки в скрытом слое имеют разные
передаточные функции, что дает три способа рассмотрения данных. Схематично
архитектура такой сети представлена на рис. 2.
Параметры сети, обеспечившие ее обучение,
следующие: количество скрытых слоев равно 3, уровень точности выхода нейронов
сети - 0.01, скорость обучения - 0.1, начальный вес - 0.3, момент - 0.1,
передаточные функции: блок 1 - логистическая (формула
1), блок 2 - Гауссова функция, имеющая вид [9]:
![]()
Блок 3 - функция
гиперболического тангенса:
![]()
Блок
4 - комплектарная Гауссова, имеющая вид:
![]()
Число нейронов в блоке 1 (входном) равно числу признаков
- 39, в выходном (блок 5) - 5, в остальных блоках - 33, по 11 в каждом блоке.
Число скрытых нейронов рассчитывали по той же формуле, что и в стандартной сети
(табл. 3). Как и в сетях, построенных на основе многослойного персептрона,
наиболее правильно классифицированы лица из 1-й и 5-й группы (коэффициент
корреляции 0,94 и 0,97 соответственно), но значительно лучшие результаты получены
для группы риска (коэффициент корреляции 0,72, а в стандартных сетях - 0,53).
Таблица 2
Результаты работы сети НСОР
|
|
Группы |
||||
|
I |
II |
III |
IV |
V |
|
|
R2: |
0,9734 |
0,9450 |
0,9928 |
0,9955 |
0,9966 |
|
Средняя квадратичная
ошибка: |
0 |
0 |
0 |
0 |
0 |
|
Средняя абсолютная ошибка |
0 |
0 |
0 |
0 |
0 |
|
Мин. абсолютная ошибка: |
0 |
0 |
0 |
0 |
0 |
|
Макс. абсолютная ошибка: |
0,008 |
0,006 |
0,008 |
0,008 |
0,006 |
|
Коэффициент корреляции r: |
0,9864 |
0,9721 |
0,9963 |
0,9977 |
0,9982 |
|
Доля с ошибкой менее 5%: |
21,186 |
11,017 |
28,814 |
21,186 |
17,797 |
|
Доля с ошибкой от 5% до
10%: |
0 |
0 |
0 |
0 |
0 |
|
Доля с ошибкой от 10% до
20%: |
0 |
0 |
0 |
0 |
0 |
|
Доля с ошибкой от 20% до
30%: |
0 |
0 |
0 |
0 |
0 |
|
Доля с ошибкой свыше 30%: |
0 |
0 |
0 |
0 |
0 |
Таблица 3
Результаты работы сети Ворда
|
|
Группы |
||||
|
I |
II |
III |
IV |
V |
|
|
R2: |
0,9448 |
0,7174 |
0,8077 |
0,8470 |
0,9683 |
|
Средняя квадратичная ошибка: |
0,009 |
0,029 |
0,040 |
0,026 |
0,005 |
|
Средняя абсолютная ошибка: |
0,026 |
0,059 |
0,072 |
0,047 |
0,024 |
|
Мин. абсолютная ошибка: |
0 |
0 |
0 |
0 |
0 |
|
Макс. абсолютная ошибка: |
0,788 |
0,951 |
1,000 |
0,921 |
0,484 |
|
Коэффициент корреляции r: |
0,9720 |
0,8470 |
0,8987 |
0,9203 |
0,9840 |
|
Доля с ошибкой менее 5%: |
17,797 |
6,780 |
22,881 |
16,102 |
16,949 |
|
Доля с ошибкой от 5% до
10%: |
1,695 |
1,695 |
0,847 |
0,847 |
0 |
|
Доля с ошибкой от 10% до
20%: |
0 |
0 |
0,847 |
0 |
0 |
|
Доля с ошибкой от 20% до
30%: |
0,847 |
0 |
0,847 |
0 |
0 |
|
Доля с ошибкой свыше 30%: |
0,847 |
2,542 |
3,390 |
4,237 |
0,847 |
Таблица 4
Показатели важности работы сетей различной архитектуры
|
N |
Переменная |
Весовой (стандарт. сеть) |
Весовой (НСОР) |
Весовой (сети Ворда) |
|
1 |
пол |
0,14 |
3,00 |
0,03996 |
|
2 |
возраст |
0,21 |
2,31 |
0,04309 |
|
3 |
N14_00 |
0,14 |
0,01 |
0,02983 |
|
4 |
N14_1 |
0,11 |
0,31 |
0,02235 |
|
5 |
A15_0 |
0,10 |
2,62 |
0,02216 |
|
6 |
N15_0 |
0,10 |
0,00 |
0,02713 |
|
7 |
N15_1 |
0,14 |
0,00 |
0,02417 |
|
8 |
I16_0 |
0,09 |
1,47 |
0,01569 |
|
9 |
N16_0 |
0,15 |
0,75 |
0,02726 |
|
10 |
N16_1W9 |
0,09 |
0,55 |
0,02240 |
|
11 |
I17_0 |
0,09 |
2,75 |
0,02327 |
|
12 |
A17_0 |
0,07 |
1,36 |
0,01419 |
|
13 |
N17_0 |
0,06 |
3,00 |
0,01069 |
|
14 |
N17_1 |
0,12 |
0,00 |
0,02358 |
|
15 |
I18_0 |
0,13 |
0,00 |
0,01558 |
|
16 |
N18_0 |
0,16 |
0,01 |
0,02604 |
|
17 |
N18_1W9 |
0,15 |
0,01 |
0,02528 |
|
18 |
N18_1W7 |
0,14 |
2,24 |
0,02359 |
|
19 |
N18_1W5 |
0,18 |
1,87 |
0,03378 |
|
20 |
N18_2W6 |
0,12 |
0,01 |
0,02854 |
|
21 |
N18_3W6 |
0,15 |
2,10 |
0,02707 |
|
22 |
N18_3W3 |
0,10 |
0,94 |
0,02320 |
|
23 |
N18_4W3 |
0,11 |
2,62 |
0,02181 |
|
24 |
N20_0 |
0,15 |
2,91 |
0,02497 |
|
25 |
N20_1 |
0,14 |
0,01 |
0,02862 |
|
26 |
N20_2W6 |
0,11 |
1,56 |
0,02626 |
|
27 |
N20_3W6 |
0,14 |
3,00 |
0,02308 |
|
28 |
N20_4W6 |
0,12 |
0,74 |
0,02244 |
|
29 |
N20_3W3 |
0,11 |
0,04 |
0,01957 |
|
30 |
N20_5W3 |
0,14 |
0,75 |
0,03177 |
|
31 |
N22_4W6 |
0,14 |
2,90 |
0,02004 |
|
32 |
N22_5W6 |
0,10 |
2,07 |
0,02516 |
|
33 |
N22_4W6 |
0,12 |
2,97 |
0,03537 |
|
34 |
N22_6W3 |
0,10 |
2,24 |
0,02020 |
|
35 |
Бс 1 |
0,13 |
1,15 |
0,03247 |
|
36 |
Бс 2 |
0,16 |
2,67 |
0,02774 |
|
37 |
Бс 3 |
0,10 |
1,47 |
0,01851 |
|
38 |
Бс 4 |
0,14 |
2,27 |
0,02466 |
|
39 |
Арт. давление |
0,26 |
1,37 |
0,04847 |
В итоге работы сетей для каждой входной переменной
были вычислены показатели важности, являющиеся грубой мерой значимости этой
переменной для выхода сети по отношению к др. входным переменным той же сети.
Чем больше показатель, тем больше вклад данной переменной
в результат работы сети. В сетях НСОР с генетическим поиском вычисляется не
показатель важности, а индивидуальный параметр сглаживания,
который можно рассматривать как показатель чувствительности для каждого входа.
Чем выше значение параметра сглаживания, тем большее влияние оказывает соответствуюещий вход на ответ сети.
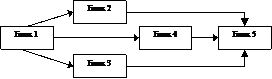
Рис. 2.
Архитектура сети Ворда
Результаты значимости признаков для сетей различной архитектуры
представлены в табл. 4: каждая
сеть выделила свои информативные признаки среди показателей ЖК, которые действуют
в рамках конкретной сети. Каждая сеть произвела классификацию индивидуумов с
высокой точностью по степени тяжести ССЗ. Наиболее информативно классификация
объектов произведена сетью с общей регрессией.
Подводя итог проведенному исследованию, можно заключить
следующее. Использование математического аппарата подтверждает высокую
диагностическую значимость показателей ЖК при ССЗ, доказанную методами
медико-биологических исследований. Применение нейросетевых
методов в медико-биологических исследованиях позволяет с высокой эффективностью
классифицировать признаки, что может быть использовано для дифференциальной
диагностики ССЗ.
Применение сетей различной архитектуры в диагностике
независимо от выделенных информативных параметров каждой сети приводит к общему
результату. Общими для нейронных сетей наиболее информативными для
дифференциальной диагностики являются параметры пола, показатели ЖК изо- и антеизостроения, ряд
представителей С20 полиеновых ЖК в
эритроцитах.
Литература
1. Galli E. et al. // British J. of Dermatology.-
1994.- Vol.
130, N 6.- P. 752-756.
2. Ma J.
et al. // Am. J. Clin. Nutr.- 1995.- Vol. 62, N 3.- P. 564-571.
3. Ohrvall
M. et al. // Eur. J. Nutr.- 1996.- Vol. 50, N 6.- P. 381-385.
4. Sarkkinen
E.S. et al. // Am. J. Clin. Nutr.- 1994.- Vol. 59, N
2.- P. 364-370.
5. Simon
J.A. et al. // Am. J. Epidemiol.- 1996.- Vol.
144, N 4.- P. 325-334.
6. Simon
J.A. et al. // Stroke.- 1995.- Vol. 26, N 5.- P.
778-782.
7. Simon
J.A. et al. // Am. J. Epidemiol.-
1995b.- Vol. 142, N 5.- Р. 469-476.
8. Specht, D. Probabilistic Neural Networks for
Classification, Mapping, or Associative Memory. Proceedings of the IEEE
International Conference on Neural Networks.- 1988.- N
1, Р. 525-532.
9. Электронный учебник по NeuroShell 2
Application
of Neuronic Networks for Selection of
Informative
Indications in Differential Diagnostics of Cardiovascular Diseases
A.I.
Abacumov, T.P. Novogorodtseva, L.V. Sorokina
Summary
Comparative
analysis of neuronic network of different structure
has been conducted for the selection of informative indications in differential
diagnostics of cardiovascular diseases (CVD). Every network chose its
informative indications in indices of fatty acids, which act within the limits
of the particular network. At the same time, every network made a
classification of individuals with a high accuracy by the degree of severity of
CDV. The most informative classification of subjects was carried out with
network of general regression.
Key words: cardiovascular
diseases, network
|
|
Сорокина
Людмила Викторовна, окончила
Дальневосточный госуниверситет. Доцент кафедры информатики и информационных
таможенных технологий Владивостокского филиала Российской таможенной академии и
соискатель при НИИ медицинской климатологии и восстановительного лечения -
Владивостокского филиала Дальневосточного НЦ физиологии и патологии дыхания СО
РАМН.
|
|
Новгородцева
Татьяна Павловна, доктор
биологических наук, зав. лабораторией биомедицинских исследований НИИ медицинской
климатологии и восстановительного лечения СО РАМН.
|
|
Абакумов
Александр Иванович, доктор
физико-математических наук, зав. лабораторией моделирования экологических
процессов Института прикладной математики ДВО РАН.