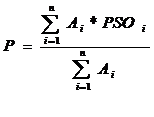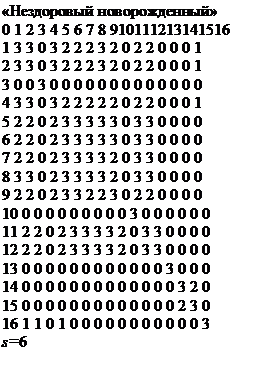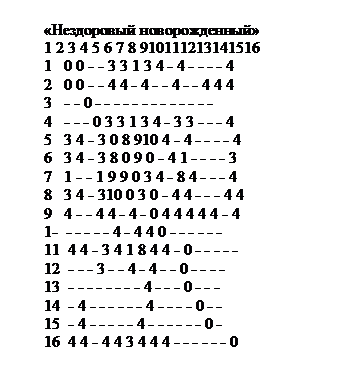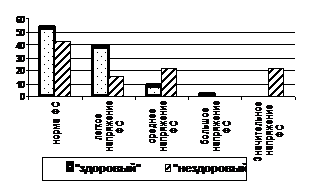ДИАГНОСТИКА ЗДОРОВЬЯ
НОВОРОЖДЕННОГО ПУТЕМ СИСТЕМНОГО АНАЛИЗА ПОКАЗАТЕЛЕЙ БЕРЕМЕННОЙ
М. В. АРТЕМЕНКО, Л.А. ЖИЛИНКОВА, Н.А.КОРЕНЕВСКИЙ
Рождение здорового
ребенка - актуальная проблема в сложившейся
демографической обстановке. Возрастает роль пренатальной диагностики прогноза
здоровья новорожденного и возникает необходимость в разработке соответствующих
компьютерных технологий на основе системного анализа функциональных состояний
(ФС). Основная гипотеза формулируется так: здоровье
новорожденного коррелирует с ФС плода,
отражаемом ФС беременной. Здесь излагаются результаты построения диагностических
решающих правил для прогнозирования рождения нездорового ребенка по данным
амбулаторного исследования беременной. В общем случае оно характеризуется
значениями регистрируемых факторов, свертка которых в определенные показатели
системной организации позволяет строить диагностические правила по "расстояниям"
между его ФС и различными кластерами в гиперпространстве. В
работах [2, 3] показано, что при различных ФС изменяются связи между
регистрируемыми показателями. Т.е. одни связи - функциональные
зависимости - теряют свою статистическую значимость, а другие ее приобретают.
Меняются структуры и параметры математических моделей, отражающие
функциональные связи.
Существует ряд подходов к оценке ФС [1, 2].
Предлагается использовать для этого показатели системной организации ФС (ПСОФС)
и максимальный градиент функциональных различий (МГФР), характеризующий
изменение количества связей между
регистрируемыми параметрами организма при развитии определенного
патологического процесса [1] (строится по матрице связности факторного
пространства, например, по корреляционной). В развитие
данной теории, с учетом возможного различного расположения диагностируемых
объектов в пространстве состояний, нами
предлагаются сл. показатели системной организации.
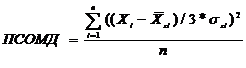 (1)
(1)
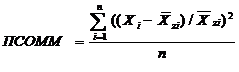 (2)
(2)
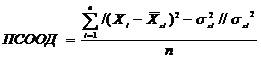 (3)
(3)
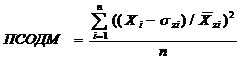 (4),
(4),
где Хi -
значение регистрируемой i-ой характеристики, n - количество характеристик, 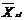 ,szi - среднее значение
и дисперсия i-ой
характеристики в базовом классе (норма). Показатель системной организации "Математическое
ожидание" - "Дисперсия" - ПСОМД - характеризует месторасположение пациента в факторном
пространстве относительно центра масс "здорового" класса, нормированного по
дисперсии здорового класса, и является модификацией ПСОФС (по Завьялову А.В.).
Показатель системной организации "Математическое ожидание" - "Математическое
ожидание" - ПСОММ - отражает положение пациента в факторном пространстве
относительно центра масс "здорового" класса, нормированного по указанному
центру масс, и является модификацией КВОЗ. Показатель системной организации по "относительной
дисперсии" - ПСООД - показывает, насколько квадратичное отклонение
расположения пациента от центра масс "здорового" класса далеко от среднего
квадратичного отклонения "здоровых" в целом, т.е. как далеко образ ФС пациента отстоит от гипероблака здоровых (или
опорного класса) в фазовом пространстве состояний. Показатель системной
организации по "дисперсии" и "математическому ожиданию" - ПСОДМ -
выявляет, насколько вариабельность значений регистрируемых факторов у пациента
далека от вариабельности таковых у "здоровых". Расширение показателей системной
организации позволяет увеличить вероятность успешности классификации по
указанным показателям в случае различных вариантов расположения диагностируемых
классов в пространстве состояний. Для получения диагностических решающих правил
предлагаются 2 подхода.
,szi - среднее значение
и дисперсия i-ой
характеристики в базовом классе (норма). Показатель системной организации "Математическое
ожидание" - "Дисперсия" - ПСОМД - характеризует месторасположение пациента в факторном
пространстве относительно центра масс "здорового" класса, нормированного по
дисперсии здорового класса, и является модификацией ПСОФС (по Завьялову А.В.).
Показатель системной организации "Математическое ожидание" - "Математическое
ожидание" - ПСОММ - отражает положение пациента в факторном пространстве
относительно центра масс "здорового" класса, нормированного по указанному
центру масс, и является модификацией КВОЗ. Показатель системной организации по "относительной
дисперсии" - ПСООД - показывает, насколько квадратичное отклонение
расположения пациента от центра масс "здорового" класса далеко от среднего
квадратичного отклонения "здоровых" в целом, т.е. как далеко образ ФС пациента отстоит от гипероблака здоровых (или
опорного класса) в фазовом пространстве состояний. Показатель системной
организации по "дисперсии" и "математическому ожиданию" - ПСОДМ -
выявляет, насколько вариабельность значений регистрируемых факторов у пациента
далека от вариабельности таковых у "здоровых". Расширение показателей системной
организации позволяет увеличить вероятность успешности классификации по
указанным показателям в случае различных вариантов расположения диагностируемых
классов в пространстве состояний. Для получения диагностических решающих правил
предлагаются 2 подхода.
Метод различий
функциональных связей. МГФР [1] позволяет качественно описать различия в
характере связей рассматриваемых классов, но не дает возможности классифицировать
отдельный организм, то есть получать решающие правила. В развитие данного
метода предлагается сл. легко автоматизирующийся алгоритм дифференциальной
диагностики:
1. ЭТАП ОБУЧЕНИЯ. Для
каждого диагностируемого класса идентифицируется набор статистически значимых в
общем случае функционалов, отражающих связи между характеристиками.
Рекомендуется начинать процесс идентификации с простейших парных линейных
зависимостей, переходя, в случае плохой эффективности решающих правил, к
нелинейным алгебраическим структурам парного характера, к множественным
линейным и нелинейным регрессионным моделям взаимосвязи, к логическим
предикатам (в случае качественных характеристик состояния организма). Получаем
конечное множество математических моделей - аппроксимантов, отражающих
взаимосвязь регистрируемых характеристик для каждого класса заболеваний. Для
упрощения вычислений рекомендуется зарегистрированные значения привести к одной
системе, например, путем нормирования - делением на средние значения одного из
класса (базового) или на средние значения характеристик здорового организма.
2. ЭТАП ДИАГНОСТИКИ. У
пациента регистрируются характеристики, вошедшие во множества полученных на
этапе обучения функционалов. Полученные значения (при необходимости
нормированные) подставляются в модели-аппроксиманты и вычисляются величины
среднего квадратичного относительного отклонения зарегистрированных значений от полученных экстраполянтов. Пациент относится к тому
диагностируемому классу, где эти величины имеют min значения. При автоматизации это означает правило "левого
нижнего угла": в координатах "математическое ожидание" - "дисперсия указанных
величин".
Метод различий
ФС - используются результаты [1], позволяющие говорить о том, что определенному ФС соответствует диапазон значений показателей системной
организации.
1. ЭТАП ОБУЧЕНИЯ. На
обучающей выборке рассчитываются значения системных показателей (формулы -
(1)-(4)) в каждом диагностируемом классе. Идентифицируем параметры Аi в формуле (5) в
интервале от 0 до 1, так, чтобы максимальным образом повысить разделяющую
возможность диапазонов полученных значений (минимизируются "зоны" перекрытия),
напри-
мер по коэффициенту
Стьюдента или по опросу экспертов, или по найденным ранее на большой выборке
оценкам вероятностей влияния i-ой
характеристики. Выбирается тот из показателей системной организации из (1)-(4),
для которого получен наилучший "разделительный" результат на экзаменационной
выборке. Формируется соответствующее решающее правило типа.
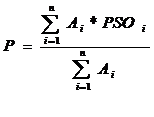 , (5)
, (5)
где Р
- выбранный показатель системной организации, PSOi - значение показателя
по i-ой характеристике.
2. ЭТАП ДИАГНОСТИКИ -
регистрируются характеристики пациента и вычисляется
значение выбранного на этапе обучения показателя системной организации. По
попаданию этой величины в соответствующий диапазон ведется диагностика.
Рассмотрим результаты
применения предлагаемых методов для синтеза диагностических правил прогноза
здоровья новорожденного по следующим характеристикам состояния организма беременной:
анализ мочи - удельный вес (х1), число
лейкоцитов в двух полях зрения - (х2, х3); анализ крови - гемоглобин (х4),
эритроциты (х5), цветовой показатель (х6), тромбоциты (х7),
лейкоциты (х8), эозонофилы (х9), палочкоядерные (х10),
сегментоядерные (х11), лимфоциты (х12), СОЭ (х13); мазок
на флору и гонорею - число лейкоцитов в
двух полях зрения - (х14, х15); сахар в крови - (х16).
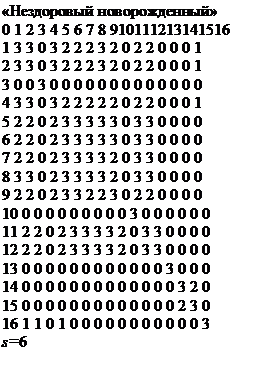 "Здоровый новорожденный"
"Здоровый новорожденный"
0 1 2 3 4 5 6 7 8 910111213141516
1 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2 0 3 3 1 1 0 0 0 0 0 0 0 0 0 0 0
3 0 3 3 1 1 0 0 0 0 0 0 0 0 0 0 0
4 0 1 1 3 2 2 1 0 0 0 0 0 1 0 0 0
5 0 1 1 2 3 0 1 0 0 0 0 0 0 0 0 0
6 0 0 0 2 0 3 0 0 0 0 0 0 1 0 0 0
7 0 0 0 1 1 0 3 0 0 0 0 0 0 0 0 0
8 0 0 0 0 0 0 0 3 0 0 0 0 1 0 0 0
9 0 0 0 0 0 0 0 0 3 0 1 0 0 0 0 0
10 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0
11 0 0 0 0 0 0 0 0 1 0 3 2 0 0 0 0
12 0 0 0 0 0 0 0 0 0 0 2 3 0 0 0 0
13 0 0 0 1 0 1 0 1 0 0 0 0 3 0 0 0
14 0 0 0 0 0 0 0 0 0 0 0 0 0 3 3 0
15 0 0 0 0 0 0 0 0 0 0 0 0 0 3 3 0
16 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3
S=1,5
Градиенты функционального отличия (по
факторам)
|
Класс
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
|
N0
|
0
|
3
|
2
|
6
|
5
|
2
|
2
|
1
|
1
|
0
|
2
|
1
|
3
|
1
|
1
|
0
|
|
N1
|
10
|
10
|
0
|
10
|
9
|
9
|
9
|
9
|
9
|
0
|
9
|
9
|
0
|
1
|
1
|
3
|
|
Градиент
|
-5
|
-2
|
1
|
0
|
0
|
-2
|
-2
|
-3
|
-3
|
-1
|
-2
|
-3
|
2
|
-1
|
-1
|
-3
|
Рис. 1. Парные линейные корреляционные отношения. Показатель МГФР = 5 -
по удельному весу показателя мочи. N0
- класс здоровых новорожденных, N1 - класс
нездоровых новорожденных, s -
сложность графа связей

"Здоровые новорожденный"
0 1 2 3 4 5 6 7 8 910111213141516
1 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2 0 3 3 1 1 0 0 0 0 0 0 0 0 0 0 0
\3 0 3 3 1 1 0 0 0 0 0 0 0 0 0 0 0
4 0 1 1 3 2 2 1 0 0 0 0 0 1 0 0 0
5 0 1 1 2 3 0 1 0 0 0 0 0 0 0 0 0
6 0 0 0 2 0 3 0 0 0 0 0 0 1 0 0 0
7 0 0 0 1 1 0 3 0 0 0 0 0 0 0 0 0
8 0
0 0 0 0 0 0 3 0 0 0 0 1 0 0 0
9 0
0 0 0 0 0 0 0 3 0 1 0 0 0 0 0
10 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0
11 0 0 0 0 0 0 0 0 1 0 3 2 0 0 0 0
12 0 0 0 0 0 0 0 0 0 0 2 3 0 0 0 0
13 0 0 0 1 0 1 0 1 0 0 0 0 3 0 0 0
14 0 0 0 0 0 0 0 0 0 0 0 0 0 3 3 0
15 0 0 0 0 0 0 0 0 0 0 0 0 0 3 3 0
16 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3
s= 1,9
Градиенты функционального отличия
|
Класс
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
|
N0
|
0
|
3
|
3
|
5
|
4
|
2
|
2
|
1
|
1
|
0
|
2
|
1
|
3
|
1
|
1
|
0
|
|
N1
|
10
|
10
|
0
|
10
|
9
|
9
|
9
|
9
|
9
|
0
|
9
|
9
|
0
|
1
|
1
|
3
|
|
Градиент
|
-5
|
-2
|
2
|
0
|
0
|
-2
|
-2
|
-3
|
-3
|
0
|
-2
|
-3
|
2
|
-1
|
-1
|
-3
|
Рис. 2. Парное корреляционное отношение (нелинейные связи) Показатель
МГФР = 5 по удельному весу показателя мочи
Матрицы связности факторного
пространства см. на рис. 1-4. В случае рис. 1 - ранжированные коэффициенты
парной корреляции, рис. 2 - ранжированные коэффициенты корреляционного
отношения, рис. 3 - ранжированные коэффициенты связности нелинейных структур из
класса математических моделей, представленных в табл.; рис. 4 - номера
идентифицированных алгебраических структур.
Ранжирование
коэффициентов связности шло по кодировке: 0 - статистической связи нет (здесь и
далее рассматривается статистическая значимость на уровне 0,05), 1 - связь
слабая, 2 - связь средняя, 3 - связь сильная.
Таблица
Структуры математических моделей парной связи
|
¦ математ.
модели
|
Вид модели
|
|
"прямая"
|
"обратная"
|
|
0
|
Y = A0 + A1*X
|
X = C + D*Y
|
|
1
|
Y = A0
+ A1 *Ln(X)
|
X = eC+D*Y
|
|
2
|
Y = 1 / (A0
+A1*X)
|
X = C + D/Y
|
|
3
|
Y = A0
* EXP(A1*X)
|
X = C + D * Ln(Y)
|
|
4
|
Y = A0 / (A1 + X)
|
X = C + D / Y
|
|
5
|
Y = A0
* X / (A0 + A1*X)
|
X = 1 / (C + D /
Y)
|
|
6
|
Y = X / (A0
+ A1 * X)
|
X = 1 / (C + D /
Y)
|
|
7
|
Y = A0
* A1X
|
X = C + D*Ln(Y)
|
|
8
|
Y = A0
* A1-X
|
X = C + D*Ln(Y)
|
|
9
|
Y = A0
+ A1 / X
|
X = 1 /(C + D *
Y)
|
|
10
|
Y = A0
+ A1 * X2
|
X = (C + D * Y)0.5
|
|
11
|
Y = A0
+ Ch(X)
|
X = C + D *
Ach(X)
|
|
12
|
Y =A0
+ Sh(X)
|
X = C + D *
Ash(X)
|
|
13
|
Y = A0 + Th(X)
|
X = C + D * Ath(X)
|

"Здоровый новорожденный"
1 2 3 4 5 6 7 8 910111213141516
1
3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2
0 3 1 3 3 0 3 3 3 0 0 0 0 0 3 3
3
0 1 3 0 1 0 0 0 0 0 1 0 0 0 0 0
4
0 3 0 3 1 2 2 0 0 0 0 0 2 1 0 0
5
0 3 1 1 3 1 2 0 0 0 0 0 0 0 0 0
6
0 0 0 2 1 3 0 0 1 0 0 0 1 0 0 0
7
0 3 0 2 2 0 3 0 0 1 0 1 0 0 0 0
8
0 3 0 0 0 0 0 3 0 0 0 0 0 0 0 0
9
0 3 0 0 0 1 0 0 3 0 0 0 1 0 0 0
10
0 0 0 0 0 0 1 0 0 3 1 0 0 0 0 1
11
0 0 1 0 0 0 0 0 0 1 3 1 0 0 0 0
12
0 0 0 0 0 0 1 0 0 0 1 3 0 0 0 0
13
0 0 0 2 0 1 0 0 1 0 0 0 3 0 0 0
14
0 0 0 1 0 0 0 0 0 1 0 0 0 3 0 0
15
0 3 0 0 0 0 0 0 0 0 0 0 0 0 3 0
16
0 3 0 0 0 0 0 0 0 1 0 0 0 0 0 3
s=3.3
Градиенты функционального отличия
|
Класс
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
|
N0
|
0
|
8
|
3
|
6
|
5
|
4
|
5
|
1
|
3
|
3
|
3
|
2
|
3
|
2
|
1
|
2
|
|
N1
|
9
|
8
|
0
|
8
|
9
|
9
|
10
|
10
|
10
|
3
|
9
|
3
|
1
|
2
|
2
|
8
|
|
Градиент
|
-6
|
2
|
3
|
1
|
-1
|
-2
|
-2
|
-6
|
-4
|
0
|
-3
|
-1
|
2
|
0
|
-1
|
-3
|
Рис. 3. Парные нелинейные регрессионные связи. Показатель МГФР = 6 по
удельному весу показателя мочи и цветовому показателю крови
Сложность графа, моделирующего структурные парные
связи между характеристиками состояния беременной, резко растет по мере
перехода к классу "рождение нездорового ребенка". Это вызвано тем, что происходящие
при этом в организме матери (и плода) патологические
изменения вызывают необходимость подключения более жестких адаптационных механизмов,
что усиливает детерминированные связи между физиологическими системами и
отражается на росте их числа (и линейного, и нелинейного плана). Переход
характеристики х1 ("удельный вес в анализе мочи") из статистически
функционально несвязанного показателя при рождении здорового ребенка в
системообразующий (имеющий max "связность") - при прогнозе
рождения нездорового ребенка м.б. применяться
в диагностике.
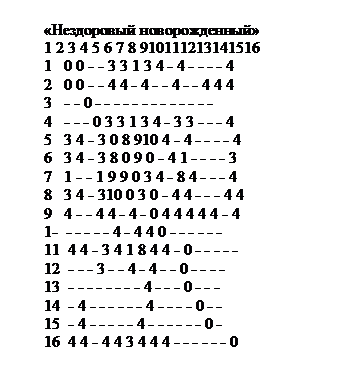
"Здоровый новорожденный"
12 3 4 5 6 7 8 910111213141516
1
0 - - - - - - - - - - - - - - -
2
- 0 4 4 4 - 4 4 4 - - - - - 4 4
3
- 4 0 - 4 - - - - - 4 - - - - -
4
- 4 - 0 4 4 4 - - - - - 4 4 - -
5
- 4 4 4 0 4 4 - - - - - - - - -
6
- - - 4 4 0 - - 9 - - - 4 - - -
7
- 4 - 4 4 - 0 - - 4 - 4 - - - -
8
- 4 - - - - - 0 - - - - - - - -
9
- 4 - - - 9 - - 0 - - - 4 - - -
1-
- - - - - - 4 - - 0 4 - - -
11
- - 4 - - - - - - 4 010 - - - -
12
- - - - - - 4 - - - 100 - - - -
13
- - - 4 - 4 - - 4 - - - 0 - - -
14
- - - 4 - - - - - 4 - - - 0 - -
15
- 4 - - - - - - - - - - - - 0 -
16
- 4 - - - - - - - 4 - - - - - 0
Рис.4. Номера парных нелинейных регрессионных
связей (по табл.: номер строки -
функция, номер столбца - аргумент в прямых зависимостях)
Построенные на базе полученных связей нелинейные
парные математические модели (рис. 4) позволили диагностировать прогноз
рождения здорового ребенка с эффективностью 0,86, прогноз рождения нездорового
ребенка - 0,82 на экзаменационной выборке. Для соблюдения условия
принадлежности обучающей и экзаменационной выборок одному закону распределения
вектор характеристик каждого пациента сворачивается в одно значение -
применялась, например, формула (1). Пациенты упорядочиваются по возрастанию полученных
значений. Задаются объемы обучающей и экзаменационной выборок. Практика
показывает, что хорошие результаты достигаются при соблюдении принципа "золотого
сечения", когда объемы обучающей и экзаменационной выборок находятся в
соотношении 0,68:0,32. Из упорядоченных данных формируются наборы указанных выборок
путем рандомизации.
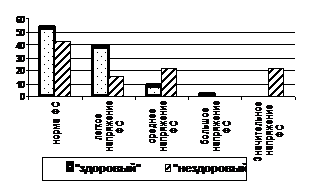
Рис. 2. Доля страт ФС у
беременных женщин
Рассмотрим результаты
исследования по 2-му предлагаемому методу - по вычислению ПСОФС - формулы
(1)-(4). На рис. 5 показано, что при
рождении нездорового ребенка состояние среднего напряжения ФС в терминологии
работы [1] по показателю (1) наблюдалось у 21% исследуемых
(в случае рождения здорового ребенка - 7,7%), очень сильное напряжение ФС
(патология) наблюдалось в 21% и никогда в "здоровом" классе. Для варианта
равенства единице значений коэффициентов Аi в (5) наилучшими
разделительными способностями (на уровне значимости 0,05, по коэффициенту
Стьюдента на экзаменационной выборке) обладали показатели: ПСОМД (с решающим
правилом: если вычисленное значение показателя превышает 0,5, то возможно
рождение нездорового ребенка - эффективность составила 0,8), ПСОДМ (с решающим
правилом: если вычисленное значение показателя больше 1,6, то возможно рождение
нездорового ребенка - эффективность составила 0,76). Эффективности применения
ПСОММ и ПСООД составили соответственно
0,25 и 0,1, что не пригодно для диагностики.
Т.о.,
на примере построения диагностических решающих правил
для классификации возможного здоровья новорожденного по данным амбулаторного
анализа беременной, показана перспективность применения рассмотренных методов
анализа функциональных различий по изменениям связей между регистрируемыми
характеристиками и показателям системной организации.
Литература
1. Завьялов А.В., Царев А.Н. Оценка
функционального состояния центральной нервной системы операторов Курской АЭС //
Актуальные вопросы медицинской науки (сборник научных трудов, посв. 60-летию
КГМУ).- Курск, 1997.- С. 284-290
2. Судаков К.В. Теория функциональных систем. -
М.: Медицинский музей, 1996.- 95 с.
3. Теория системогенеза / Под
ред. К.В. Судакова.- М.: Горизонт, 1997.- 567 с.
Diagnostics of Newborn Health by the System Analysis
of Parameters of a Pregnant Woman
М. V.
Artyomenko, L.A. Gilinkova, N. A. Korenevskiy
Summary
The authors
consider questions of application of parameters of a system organization of a
body`s functional state to construction of diagnostic decisive rules of
differential prognostication of newborn health on the base of results of outpatient
inspection of a pregnant woman. Methods and algorithms of synthesis of decisive
rules based on the analysis of functional connections and states of the
pregnant woman are considered. For the first time it is offered: a ranging
approach to construction of diagnostic rules on parameters of system
organization and classification of a condition of the patient by deviations in
functional connections between the registered characteristics in diagnosed
classes. The results of the practical proof of offered methods are given.
Key words: functional state,
system organization
Артеменко Михаил Владимирович
- канд. биол. наук, доцент кафедры биомедицинской инженерии КГТУ,
член-корреспондент МАНЭБ. Имеет более 50 публикаций, в
т.ч. 1 монография
Жилинкова Людмила Анатольевна,
преподаватель кафедры общеинженерной подготовки Курского госмедуниверситета,
аспирант кафедры БМИ КурскГТУ. Имеет 8 публикаций.
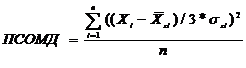 (1)
(1)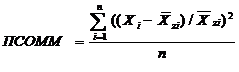 (2)
(2)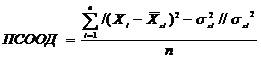 (3)
(3)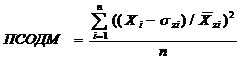 (4),
(4),![]() ,szi - среднее значение
и дисперсия i-ой
характеристики в базовом классе (норма). Показатель системной организации "Математическое
ожидание" - "Дисперсия" - ПСОМД - характеризует месторасположение пациента в факторном
пространстве относительно центра масс "здорового" класса, нормированного по
дисперсии здорового класса, и является модификацией ПСОФС (по Завьялову А.В.).
Показатель системной организации "Математическое ожидание" - "Математическое
ожидание" - ПСОММ - отражает положение пациента в факторном пространстве
относительно центра масс "здорового" класса, нормированного по указанному
центру масс, и является модификацией КВОЗ. Показатель системной организации по "относительной
дисперсии" - ПСООД - показывает, насколько квадратичное отклонение
расположения пациента от центра масс "здорового" класса далеко от среднего
квадратичного отклонения "здоровых" в целом, т.е. как далеко образ ФС пациента отстоит от гипероблака здоровых (или
опорного класса) в фазовом пространстве состояний. Показатель системной
организации по "дисперсии" и "математическому ожиданию" - ПСОДМ -
выявляет, насколько вариабельность значений регистрируемых факторов у пациента
далека от вариабельности таковых у "здоровых". Расширение показателей системной
организации позволяет увеличить вероятность успешности классификации по
указанным показателям в случае различных вариантов расположения диагностируемых
классов в пространстве состояний. Для получения диагностических решающих правил
предлагаются 2 подхода.
,szi - среднее значение
и дисперсия i-ой
характеристики в базовом классе (норма). Показатель системной организации "Математическое
ожидание" - "Дисперсия" - ПСОМД - характеризует месторасположение пациента в факторном
пространстве относительно центра масс "здорового" класса, нормированного по
дисперсии здорового класса, и является модификацией ПСОФС (по Завьялову А.В.).
Показатель системной организации "Математическое ожидание" - "Математическое
ожидание" - ПСОММ - отражает положение пациента в факторном пространстве
относительно центра масс "здорового" класса, нормированного по указанному
центру масс, и является модификацией КВОЗ. Показатель системной организации по "относительной
дисперсии" - ПСООД - показывает, насколько квадратичное отклонение
расположения пациента от центра масс "здорового" класса далеко от среднего
квадратичного отклонения "здоровых" в целом, т.е. как далеко образ ФС пациента отстоит от гипероблака здоровых (или
опорного класса) в фазовом пространстве состояний. Показатель системной
организации по "дисперсии" и "математическому ожиданию" - ПСОДМ -
выявляет, насколько вариабельность значений регистрируемых факторов у пациента
далека от вариабельности таковых у "здоровых". Расширение показателей системной
организации позволяет увеличить вероятность успешности классификации по
указанным показателям в случае различных вариантов расположения диагностируемых
классов в пространстве состояний. Для получения диагностических решающих правил
предлагаются 2 подхода.